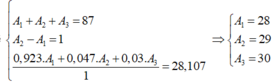Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi số khối của X lần lượt là A1, A2, A3
Ta có hệ
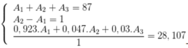
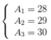

Gọi a,b lần lượt là số khối của đvi 1 và đvi 2
Theo đề ta có:
\(63,5=\dfrac{a\cdot25+b\cdot75}{100}\\ < =>25a+75b=6350\\ < =>25\left(a+3b\right)=6350\\ < =>a+3b=254\left(^1\right)\)
Lại có tổng số khổi của 2 đvi là 128
\(< =>a+b=128\left(^2\right)\)
Từ (1) và (2) giải hệ ta được:
\(a=65;b=63\)
Vậy Số khổi của đvi 1 là 65
số khối của đvi 2 là 63

Gọi A1 , A2, A3 lần lượt là số khối của các đồng vị X1 , X2, X3
N1 , N2, N3 lần lượt là số nuetron của các đồng vị X1 , X2, X3
%X1 = 100% - (92,23% - 4,67 %) = 3,1 (%)
Theo đề ta có : N2 = N1 + 1
<=> A2 = A1 + 1 (I)
A1 + A2 + A3 = 87 (II)
Mặt khác : 92,23A1 + 4,67A2 + 3,1A3 = 28,0855*100 (III)
Giai hệ (I) , (II) , (III) ta được
A1 = 28
A2 = 29
A3 = 30
ngoài ra : N1 = P <=> Z = N1 <=> A1 = 2Z
=> Z = A1 / 2 = 28 / 2 = 14 (Si)
X là Silic (Si)
Kí hiệu của X1 : 1428Si
Kí hiệu của X2 : 1429Si
Kí hiệu của X3 : 1430Si