Question

[Pham Trong Bach]

Hệ bất phương trình  2 x + 4 < 0 m x + 1 > 0  có tập nghiệm là  - ∞ ; - 2  khi và chỉ khi

A.  m ≤ 0

B.  m < 0

C.  m > 0

D.  m < - 1 2

Answer 1

[Cao Minh Tâm]

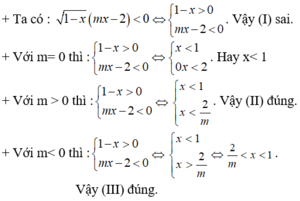
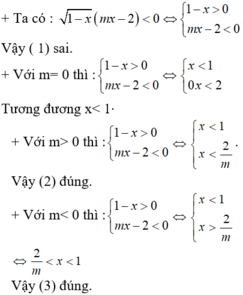
Ta có:  2x +  4 < 0 khi x < - 2.

* Xét mx + 1 >  0   (*)

   + Nếu m = 0 thì (*) trở thành: 0x + 1 >0 (luôn đúng).

  + Nếu m > 0 thì  * ⇔ m x > - 1 ⇔ x > - 1 m

Suy ra, tập nghiệm của hệ bất phương trình không thể  - ∞ ; - 2

  + Nếu m < 0 thì  * ⇔ m x > - 1 ⇔ x < - 1 m

Để hệ bất phương trình có tập nghiệm là  - ∞ ; - 2  khi và chỉ khi :

- 1 m > - 2 ⇔ - 1 + 2 m m > 0 ⇔ - 1 + 2 m < 0   ( vì m < 0)

⇔ 2 m < 1 ⇔ m < 1 2

Kết hợp điều kiện m < 0 ta được: m < 0

Từ các trường hợp trên suy ra:   m ≤ 0 .