Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

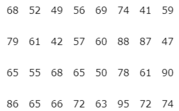
Sắp xếp lại:
5 | 31 | 37 | 43 | 43 | 57 | 62 | 63 | 78 | 80 | 91 |
Khoảng biến thiên R=91-5=86
Ta có: \({Q_2} = 57,{Q_1} = 37,{Q_3} = 78\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 78 - 37 = 41\)
Số trung bình \(\overline X \approx 53,64\)
Ta có bảng sau:
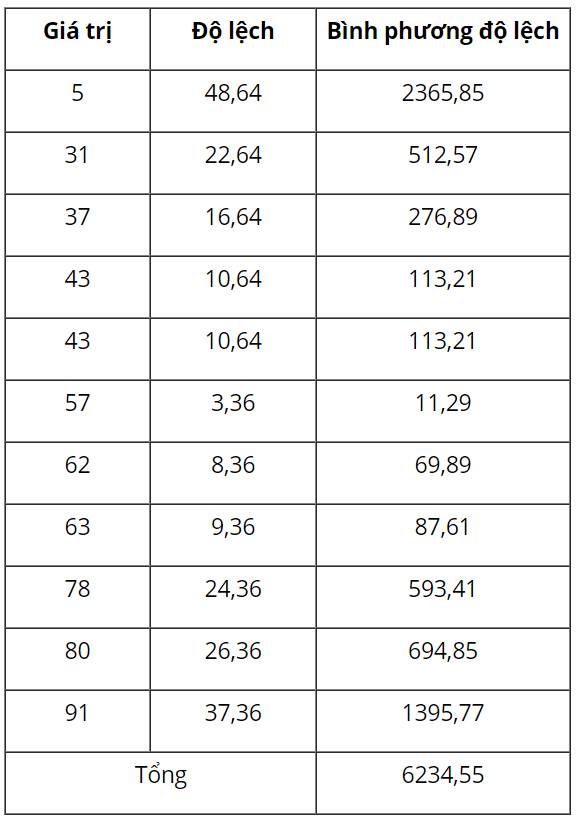
Độ lệch chuẩn là 79
Môn Tiếng Anh:
Sắp xếp lại:
37 | 41 | 49 | 55 | 57 | 62 | 64 | 65 | 65 | 70 | 73 |
Khoảng biến thiên R=73-37=36
Ta có: \({Q_2} = 62,{Q_1} = 49,{Q_3} = 65\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 65 - 49 = 16\)
Số trung bình \(\overline X = 58\)
Ta có bảng sau:
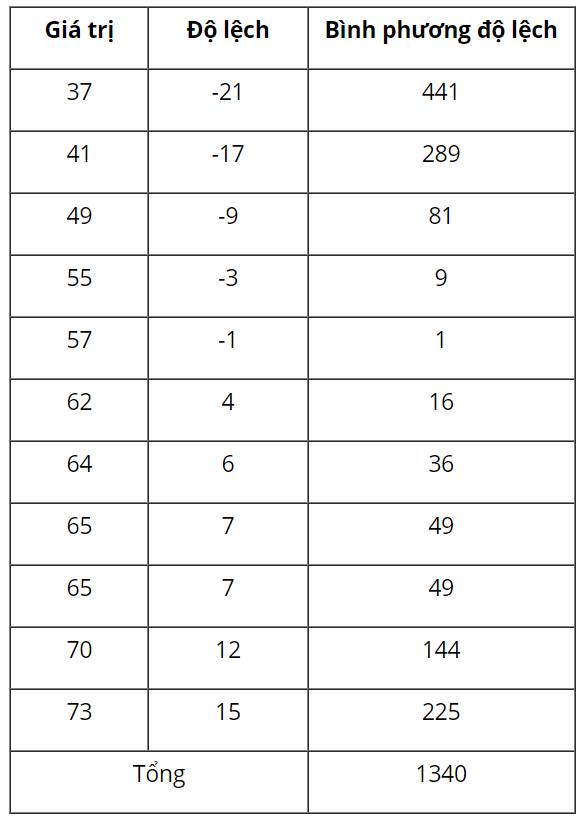
Độ lệch chuẩn là 36,6
Từ các số trên ta thấy mức độ học tập môn Tiếng Anh không đều bằng môn Toán.Độ lệch chuẩn là 36,6

a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)

Số trung bình | \(\overline x \) | 1,632184 |
Phương sai \(({S^2})\) | \({\sigma ^2}x\) | 1,106091 |
Độ lệch chuẩn \((S)\) | \(\sigma x\) | 1,051708 |
Phương sai hiệu chỉnh \(({\widehat s^2})\) | \({s^2}x\) | 1,118952 |
Cỡ mẫu | \(n\) | 87 |
Giá trị nhỏ nhất | \(\min \left( x \right)\) | 0 |
Tứ phân vị thứ nhất | \({Q_1}\) | 1 |
Trung vị \(({M_e})\) | \(Med\) | 2 |
Tứ phân vị thứ ba | \({Q_3}\) | 2 |
Giá trị lớn nhất | \(\max (x)\) | 5 |

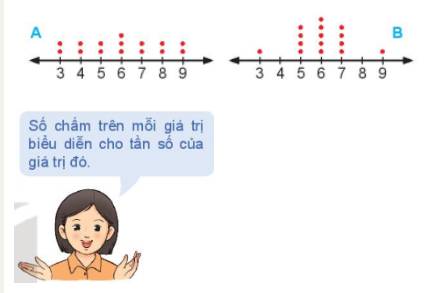
a) Cả 2 mẫu đều có n=15.
Ta có cả 2 mẫu đều có giá trị nhỏ nhất là 3, giá trị lớn nhất là 9
Do đó cả 2 mẫu cùng khoảng biến thiên.
Cả 2 biểu đồ này có dạng đối xứng nên giá trị trung bình của hai mẫu A và B bằng nhau.
b) Từ biểu đồ ta thấy, mẫu A có các số liệu đồng đều và ổn định hơn mẫu B nên phương sai của mẫu A nhỏ hơn mẫu B.

Cách 1:
+ Giá trị đại diện mỗi lớp: c 1 = 18 ; c 2 = 22 ; c 3 = 26 ; c 4 = 30 ; c 5 = 34
+ Số trung bình cộng:
x = n 1 c 1 + n 2 c 2 + n 3 c 3 + n 4 c 4 + n 5 c 5 n 1 + n 2 + n 3 + n 4 + n 5 = 10 . 18 + 12 . 22 + 14 . 26 + 9 . 30 + 5 . 34 50 ≈ 25
+ Độ lệch chuẩn:
s = s 2 = 10 18 - 25 2 + 12 22 - 25 2 + 14 26 - 25 2 + 9 30 - 25 2 + 5 34 - 25 2 50
≈ 5 , 0
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập ![]() (vào chế thống kê).
(vào chế thống kê).
+ Nhập ![]() (hiển thị cột tần số).
(hiển thị cột tần số).
+ Nhập ![]() (nhập giá trị).
(nhập giá trị).
+ Nhập ![]() (nhập tần số), sau đó ấn
(nhập tần số), sau đó ấn ![]() .
.
+ Nhập ![]()
⇒ δ x = 4 , 983813801
(Lưu ý: Đối với Ví dụ 2, phương sai s 2 = 24 , 9 ).
Đáp án C.

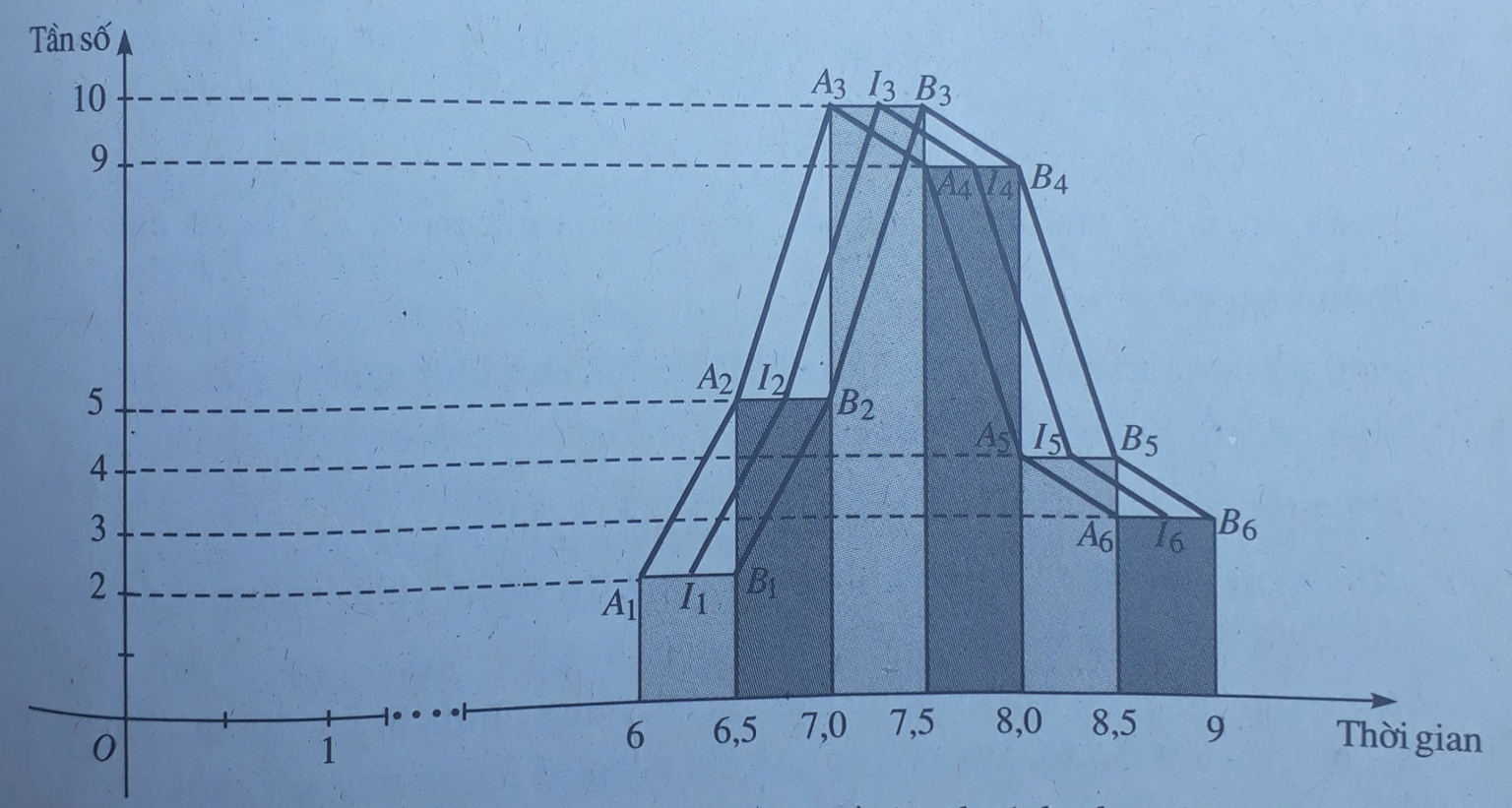
Các đỉnh của đường gấp khúc tần số có tọa độ là ( c i ; n i ), với c i là giá trị đại diện của lớp thứ i, n i là tần số của lớp thứ i. Từ đó suy ra: các đỉnh của đường gấp khúc tần số là các trung điểm của các cạnh phía trên của các cột (các hình chữ nhật) của biểu đồ tần số hình cột
Đường gấp khúc I 1 I 2 I 3 I 4 I 5 I 6 với I 1 , I 2 , I 3 , I 4 , I 5 , I 6 lần lượt là trung điểm của các đoạn thẳng A 1 B 1 , A 2 B 2 , A 3 B 3 , A 4 B 4 , A 5 B 5 , A 6 B 6

Ta có n=2+4+6+12+8+3=35, lẻ.
Trung vị là học sinh thứ 18
Ta thấy 2+4+6<18<2+4+6+12
=> \({Q_2} = 3\)
Ta tìm \({Q_1}\) là trung vị của nửa số liệu bên trái \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên trái \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9:
Ta thấy 2+4<9<2+4+6
=>\({Q_1} = 2\)
Ta tìm \({Q_3}\) là trung vị của nửa số liệu bên phải \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên phải \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9 trong 17 học sinh và là học sinh thứ 9+18=27 trong 35 học sinh.
Ta thấy 2+4+6+12<27<2+4+6+12+8
=>\({Q_3} = 4\)


Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.

Ta lập bảng phân bố tần số ghép lớp:
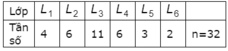
Số học sinh có số điểm trong nửa khoảng [50;80) là 6 + 11 + 6 = 23.

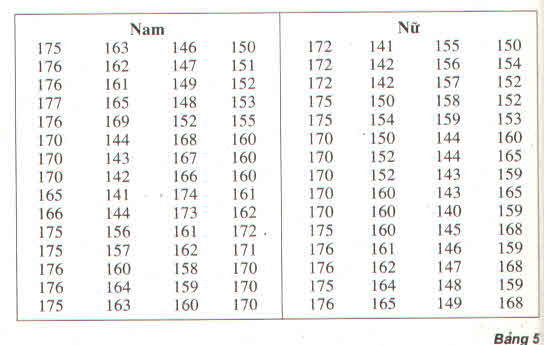
Lớp A:
Trung bình cộng lớp A: \(\overline {{X_A}} = \frac{{148}}{{25}} = 5,92\)
Bảng tần số:
Điểm
2
3
4
5
6
7
8
9
Số HS
2
2
2
5
2
6
3
3
Do n=25 nên trung vị: số thứ 13
Do 2+2+2+5+2=13
=> Trung vị là 6.
Mốt là 7 do 7 có tần số là 6 (cao nhất)
Lớp B:
Trung bình cộng lớp B: \(\overline {{X_B}} = \frac{{157}}{{25}} = 6,28\)
Bảng tần số:
Điểm
3
4
5
6
7
8
9
10
Số HS
2
2
4
5
7
2
2
1
Do n=25 nên trung vị: số thứ 13
Do 2+2+4+5=13
=> Trung vị là 6.
Mốt là 7 do 7 có tần số là 7 (cao nhất)
Trừ số trung bình ra thì trung vị và mốt của cả hai mẫu số liệu đều như nhau
=> Hai phương pháp học tập hiệu quả như nhau.