Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các trường hợp bằng nhau của tam giác vuông:
-Hai cạnh góc vuông
-Cạnh góc vuông-góc nhọn kề
-Cạnh huyền-góc nhọn
-Cạnh huyền-cạnh góc vuông

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

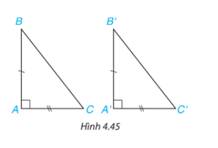
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
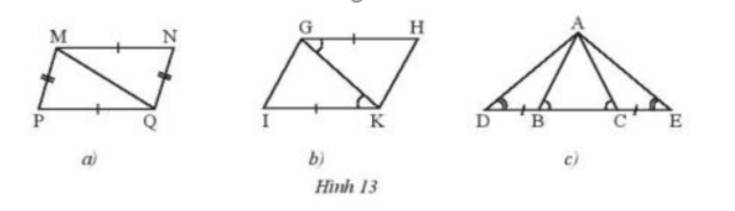

a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)
b) Ta thấy tam giác GHK = tam giác GIK (c-g-c)
c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)
Tam giác ADC = tam giác AEB (g-c-g)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
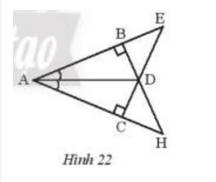

+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
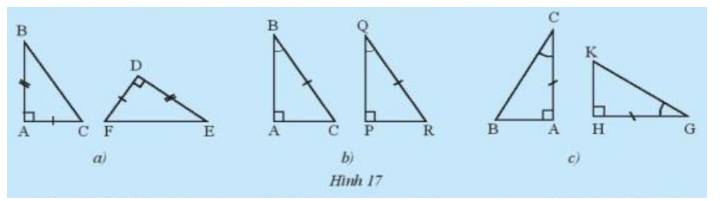
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)