Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
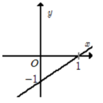
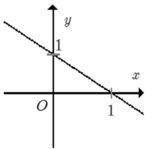
Đồ thị đi xuống từ trái sang phải => hệ số góc a < 0. Loại A, C.
Đồ thị hàm số cắt trục tung tại điểm (0; 1).

Đáp án D
Nhận xét:
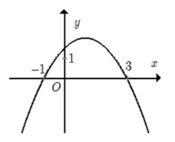
Parabol có bề lõm hướng xuống. Loại đáp án A, C.
Parabol cắt trục hoành tại 2 điểm (3; 0) và (−1; 0). Xét các đáp án B và D, đáp án D thỏa mãn.

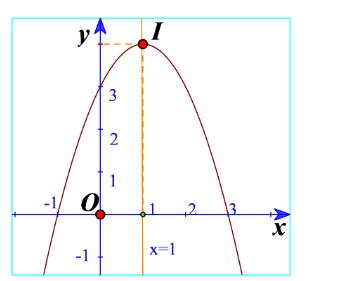
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
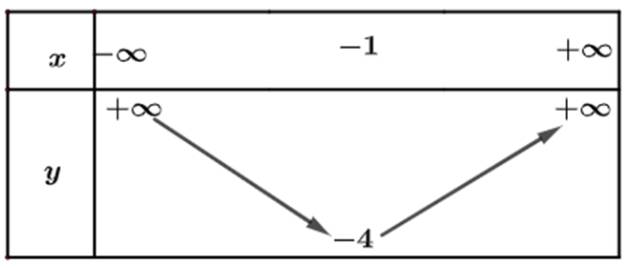
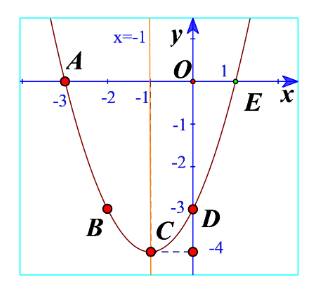
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
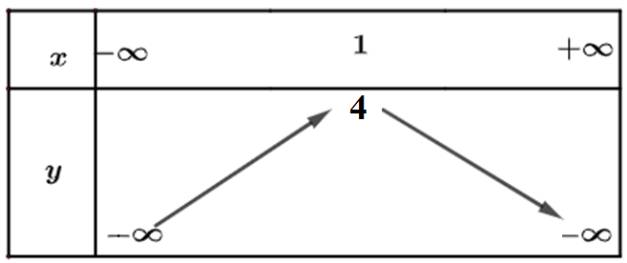

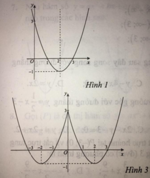
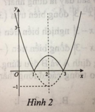
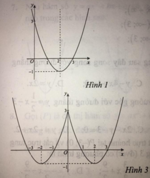
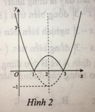
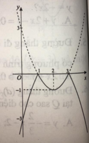
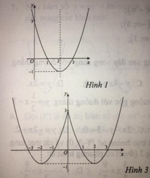
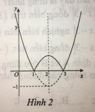
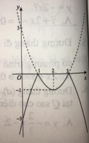
Hàm số y = x 2 - 4 x + 3 là hàm số chẵn nhận trục Oy làm trục đối xứng nên chỉ có hình 3 thỏa mãn .

Ta có: y = x 2 - 4 x + 3 = x 2 - 4 x + 3 k h i x 2 - 4 x + 3 ≥ 0 - x 2 - 4 x + 3 k h i x 2 - 4 x + 3 < 0
Cách vẽ đồ thị y = x 2 - 4 x + 3
+ Vẽ đồ thị hàm số y = x2 – 4x + 3 (C).
+ Giữ nguyên phần đồ thị (C) phía trên trục hoành
Lấy đối xứng phần dưới trục hoành qua trục hoành; xóa phần đồ thị (C) dưới trục hoành.
Khi đó, ta được đồ thị hàm số y = x 2 - 4 x + 3 .
Chọn B

Đồ thị của hàm số y = x2 – 4x + 3 là đường cong parabol nên chọn A.
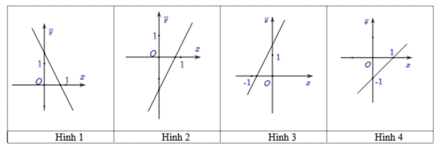
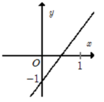



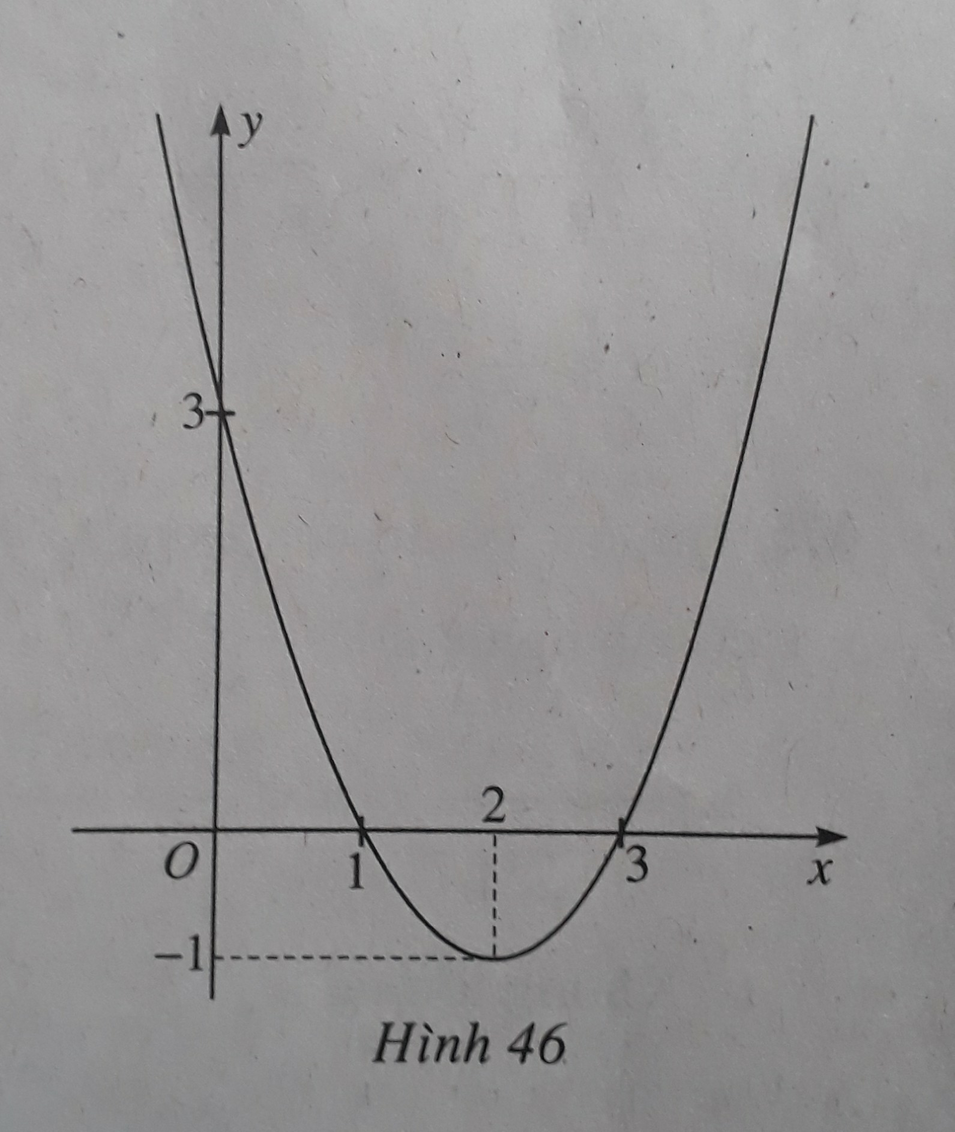
Đáp án B