Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số y = f(x) = x4 - 3x2 + 1 có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa f(-x) = (-x)4 - 3(-x)2 + 1 = x4 - 3x2 + 1 = f(x), nên y = f(x) là hàm số chẵn.
b) Hàm số y = g(x) = -2x3 + x có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa g(-x) = -2(-x)3 + (-x) = 2x3 - x = -g(x), nên y = g(x) là hàm số lẻ.
c) Hàm số y = h(x) =|x + 2|- |x - 2 | có tập xác định D là R, do đó ∀ x ∈ D thì –x ∈ D, hơn nữa h(-x) = | -x + 2| -|-x – 2|= |x - 2| - |x + 2|= -(|x + 2| - |x - 2 |) = -h{x)
Vì vậy y = h(x) là hàm số lẻ.
d) Chứng minh tương tự ta có y = |2x + 1| + |2x — 1| là hàm số chẵn.

a.
\(D=R\)
\(f\left(-x\right)=\left|-2x-3\right|+\left|-2x+3\right|=\left|2x+3\right|+\left|2x-3\right|=f\left(x\right)\)
Hàm chẵn
b.
\(D=R\)
\(f\left(-x\right)=\dfrac{\left(-x\right)^3+\left(-x\right)}{\left(-x\right)^4+1}=\dfrac{-x^3-x}{x^4+1}=-\dfrac{x^3+x}{x^4+1}=-f\left(x\right)\)
Hàm lẻ

Tập xác định của hàm số y = 1 x + 3 là D = ℝ \ - 3 .
Nhận thấy 3 ∈ D, nhưng -3 ∉ D.
Vậy hàm số y = 1 x + 3 không chẵn và không lẻ.
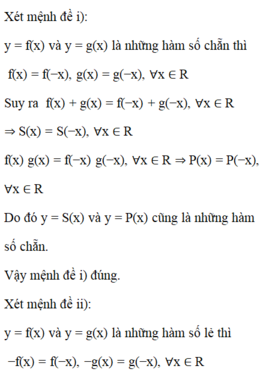
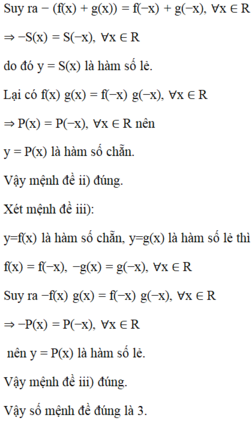
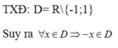
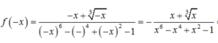
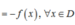
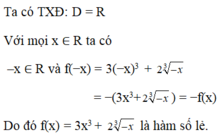

Chọn D