Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo :
hai vòi nước cùng chảy vào một cái bể không có nước,trong 4h48' sẽ đầy bể.nếu mở vòi thứ nhất trong 3h và vòi thứ hai trong 4h thì được 3/4 bể nước.hỏi mỗi vòi khác chảy thì trong bao lâu mới đầy bể?
Gọi năng suất vòi 1 là x (x>0) (năng suất ở đây hiểu là sau 1 giờ thì vòi 1 chảy được 1 lượng nước nào đó). Gọi năng suất vòi 2 là y (y>0) => năng suất chung cả hai vòi là x+y. Do sau 4,8 giờ (4h48') thì 2 vòi chảy cùng đầy bể nên 1 giờ thì 2 vòi chảy được lượng nước là 1/4,8 bể = 5/24 bể => x+y =5/24 (1). Do mở vòi thứ nhất trong 3h và vòi thứ hai trong 4h thì được 3/4 bể nước nên ta có phương trình 3x+4y=3/4 (bể) (2), từ (1) và (2) => ta có hệ phương trình x+y =5/24 và 3x+4y=3/4. Giải hệ phương trình này ta được x=1/12 và y=1/8. => thời gian chảy đẩy bể của vòi 1 là 1/x = 12h, và tương tự thì vòi 2 là 8h
Gọi thời gian chảy riêng của vòi 1 và vòi 2 lần lượt là a,b
Theo đề, ta có hệ:
1/a+1/b=1/6 và 10/a+4/b=1
=>a=18; b=9
Gọi thời gian chảy 1 mình đầy bề của vòi 1 và vòi 2 lần lượt là x và y giờ (x;y>0)
Trong 1 giờ hai vòi lần lượt chảy được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần bể
Do 2 vòi cùng chảy trong 6h đầy bể nên: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)
Hai vòi chảy 2h và khóa vòi 1, để vòi 2 chảy 12 giờ đầy bể nên: \(2\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+12.\dfrac{1}{y}=1\)
\(\Rightarrow\dfrac{2}{x}+\dfrac{14}{y}=1\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{14}{y}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{9}\\\dfrac{1}{y}=\dfrac{1}{18}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=9\\y=18\end{matrix}\right.\)
Để tìm ra thời gian mỗi vòi chảy một mình thì đầy bể, ta có thể sử dụng phương pháp sau:
Tìm ra thời gian hai vòi chảy chung là bao lâu: 4 giờ 48 phút (thời gian hai vòi chảy chung để đầy bể).
Tìm ra thời gian hai vòi chảy riêng là bao lâu: 9 giờ + 5 giờ 12 phút = 14 giờ 12 phút (thời gian hai vòi chảy riêng để đầy bể)
Tìm ra thời gian mỗi vòi chảy một mình: 14 giờ 12 phút / 2 = 7 giờ 6 phút (thời gian mỗi vòi chảy một mình để đầy bể)
Vậy, mỗi vòi chảy một mình trong 7 giờ 6 phút thì đầy bể.
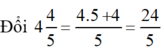
Cách 1.
Gọi thời gian để vòi thứ nhất, vòi thứ 2 chảy 1 mình đầy bể là x (h), y (h).
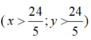
+ Một giờ vòi thứ nhất chảy được :1/x ( bể )
Một giờ vòi thứ hai chảy được :1/y ( bể )
+ Hai vòi nước cùng chảy vào một bể nước cạn (không có nước) thì sau 4 4 5 = 24 5 giờ đầy bể.
=> Một giờ cả hai vòi chảy được :
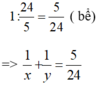
* Nếu ban đầu mở vòi 1 và 9 giờ sau mở thêm vòi 2 thì sau 6/5 (h) đầy bể. Khi đó, thời gian vòi 1 chảy là : 9 + 6 5 = 51 5 ( h ) .
Thời gian vòi 2 chảy là 6/5 (h)
Vậy nếu ngay từ đầu chỉ mở vòi 2 thì sau 8 giờ sẽ đầy bể.
Cách 2.
Gọi lượng nước vòi thứ nhất và vòi thứ hai chảy một mình trong 1 giờ lần lượt là x (bể) và y (bể).
Điều kiện 0 < x, y < 1.
+ Cả hai vòi cùng chảy trong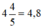 
giờ đầy 1 bể nên ta có phương trình: 4,8x + 4,8y = 1.
+ Nếu mở vòi thứ nhất trong 9 giờ thì chảy được 9x (bể)
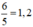giờ sau mở thêm vòi thứ hai thì chảy thêm được: 1,2 (x + y) (bể)
Khi đó bể đầy nên ta có phương trình: 9x + 1,2(x + y) = 1.
Ta có hệ phương trình
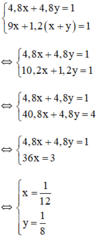
⇒ một giờ vòi hai chảy một mình được 1/8 bể
Vậy nếu ngay từ đầu chỉ mở vòi thứ hai thì sau 8 giờ sẽ đầy bể.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Sửa đề: Chỉ được 1/3 bể
Gọi thời gian chảy một mình đầy bể của vòi 1 là x(giờ), thời gian chảy một mình đầy bể của vòi 2 là y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, vòi 1 chảy được \(\dfrac{1}{x}\left(bể\right)\)
Trong 1 giờ, vòi 2 chảy được \(\dfrac{1}{y}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được 1/18(bể)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\left(1\right)\)
Trong 4 giờ, vòi 1 chảy được \(4\cdot\dfrac{1}{x}=\dfrac{4}{x}\left(bể\right)\)
Trong 7 giờ, vòi 2 chảy được \(7\cdot\dfrac{1}{y}=\dfrac{7}{y}\left(bể\right)\)
Theo đề, ta có: \(\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{2}{9}\\\dfrac{4}{x}+\dfrac{7}{y}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{3}{y}=\dfrac{2}{9}-\dfrac{1}{3}=\dfrac{-1}{9}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=27\\\dfrac{1}{x}=\dfrac{1}{18}-\dfrac{1}{27}=\dfrac{1}{54}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=54\\y=27\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian chảy một mình đầy bể của vòi 1 và vòi 2 lần lượt là 54 giờ và 27 giờ
Gọi x(h) là thời gian vòi 1 chảy một mình đầy bể
Gọi y(h) là thời gian vòi 2 chảy một mình đầy bể
(Điều kiện: x>12; y>12)
Trong 1 giờ, vòi 1 chảy được: \(\dfrac{1}{x}\)(bể)
Trong 1 giờ, vòi 2 chảy được: \(\dfrac{1}{y}\)(bể)
Trong 1 giờ, hai vòi chảy được: \(\dfrac{1}{12}\)(bể)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)(1)
Vì khi vòi 1 chảy trong 3 giờ và vòi 2 chảy thêm 18 giờ mới đầy bể nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{18}{y}=1\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{3}{x}+\dfrac{18}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{1}{4}\\\dfrac{3}{x}+\dfrac{18}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-15}{y}=\dfrac{-3}{4}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=20\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{20}=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=20\end{matrix}\right.\)(thỏa ĐK)
Vậy: Vòi 1 cần 30 giờ để chảy đầy bể khi chảy một mình
Vòi 2 cần 20 giờ để chảy đầy bể khi chảy một mình
bổ sung là vòi 1 chảy 3h xong khóa lại rồi mới chỉ mở vòi 2 trong 18h ạ