Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc ô tô khởi hành từ tỉnh A là x (km/h)
Gọi vận tốc ô tô khởi hành từ tỉnh B là y (km/h)
(ĐK: \(x>y>0\) )
Đổi: \(5h22'=\dfrac{161}{30}h,40'=\dfrac{2}{3}h\)
Hai ô tô đi ngược chiều và gặp nhau sau 5h nên ta có phương trình:
\(5x+5y=400\)
Quãng đường ô tô từ tỉnh A đi được đến lúc gặp nhau là: \(\dfrac{161}{30}x\left(km\right)\)
Quãng đường ô tô từ tỉnh B đi được đến lúc gặp nhau là: \(\dfrac{161}{30}y-\dfrac{2}{3}y=\dfrac{47}{10}y\left(km\right)\)
Do đó ta có phương trình:
\(\dfrac{161}{30}x+\dfrac{47}{10}y=400\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{161}{30}x+\dfrac{47}{10}y=400\\5x+5y=400\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=36\\y=44\end{matrix}\right.\)
Vậy vận tốc ô tô khởi hành từ tỉnh A là 36 (km/h)
Vận tốc ô tô khởi hành từ tỉnh B là 44 (km/h).

5h22p-40p=4h42p=4,7h
5h22p=161/30h
Gọi vận tốc xe 1 và xe 2 lần lượt là a,b(a>b)
Theo đề, ta có: 5(a+b)=400 và 161/30b+4,7a=400
=>a=44 và b=36

gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
→x=36 ,y=44 (km/h)

Đáp án A
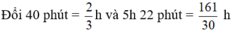
Gọi vận tốc của xe nhanh là x km/h
Gọi vận tốc của xe chậm là y km/h (điều kiện: x> y > 0)
Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau nên ta có phương trình

Vậy vận tốc của xe nhanh là 44 km/h
Vận tốc của xe chậm là 36 km/h.
gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
→x=36 ,y=44 (km/h)
=>A

Gọi thời gian dự định đi từ A đến B là x ( giờ) ( x>0)
=> quãng đường AB : 12x
1h20'=1/3=4/3h
Theo bài ra, ta có pt:
\(\frac{1}{3}.\frac{12x}{2}+\frac{20}{60}+\frac{2}{3}.\frac{12x}{36}=x-\frac{4}{3}\)
giải ra được \(x=\frac{15}{4}\) (giờ)
Vậy độ dài quãng đường AB : 12.\(\frac{15}{4}=45\left(km\right)\)
gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
Theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
Vậy : x=36 ,y=44 (km/h)

Lời giải:
Đổi 40' = $\frac{2}{3}$ giờ
Gọi vận tốc xe nhanh là a và xe chậm là b (đơn vị: km/h)
Theo bài ra ta có:
$a+b=400:5=80(1)$
Kể từ khi xe nhanh xuất phát, hai xe đi ngược chiều nhau 1 quãng đường có độ dài $400-\frac{2}{3}b$ (km). Hai xe gặp nhau sau $5h22'=\frac{161}{30}$ giờ. Khi đó ta có:
$a+b=(400-\frac{2}{3}b):\frac{161}{30}(2)$
Từ $(1); (2)\Rightarrow (400-\frac{2}{3}b): \frac{161}{30}=80$
$\Rightarrow b=-44$ (km) (vô lý)

Bg: Gọi vận tốc ôtô khởi hành từ tỉnh A Ɩà x (km/h)
Gọi vận tốc ôtô khởi hành từ tỉnh B Ɩà Ɩà y (km/h)
(ĐK: x > y > 0).Đổi 5h22′ = 161/30h, 40′ = 2/3h
Hai ôtô đi ngược chiều nhau ѵà gặp nhau sau 5h nên ta có phương trình 5x + 5y = 400
Quãng đường mà ôtô từ đỉnh A đi được đến lúc gặp nhau Ɩà:
161/30x (km)
Quãng đường mà ôtô từ đỉnh B đi được đến lúc gặp nhau Ɩà:
161/30y – 2/3y = 47/10y (km)
Do đó ta có phương trình:
161/30x + 47/10y = 400
=> Hệ phương trình: {161/30x + 47/10y = 400; 5x + 5y = 400}
⇔ {5x + 5y = 400; 161x + 141y = 12000}
⇔ {161x + 161y = 12880; 161x + 141y = 12000}
⇔ {y = 44; 161x + 141y = 12000} ⇔ {x = 36; y = 44} (thỏa mãn)
⇒ Vận tốc c̠ủa̠ ôtô khởi hành từ A Ɩà 36 (km/h).
Vận tốc c̠ủa̠ ôtô khởi hành từ B Ɩà 44 (km/h).

Gọi x (km/h) là vận tốc của xe chạy nhanh, y (km/h) là vận tốc xe chạy chậm.
Theo đề : Hai xe khởi hành cùng lúc, đi ngược chiều và gặp nhau sau 5h, ta có :
\(5\left(x+y\right)=400\Leftrightarrow x+y=80\)(1)
Theo đề vế sau, xe đi chậm đến lúc gặp nhau sau 5h22' \(=\dfrac{161}{30}\left(h\right)\)
=> Xe nhanh đi hết \(\dfrac{161}{30}-\dfrac{2}{3}=\dfrac{141}{30}\left(h\right)\)
\(\Leftrightarrow\dfrac{141}{30}x+\dfrac{161}{30}y=400\left(2\right)\)
(1) , (2) Ta có hpt :
\(\left\{{}\begin{matrix}x+y=80\\\dfrac{141}{30}x+\dfrac{161}{30}y=400\end{matrix}\right.\)
Giải hệ => \(\left\{{}\begin{matrix}x=44\\y=36\end{matrix}\right.\).
Vậy xe nhanh đi vs vận tốc 44 km/h, xe chậm 36 km/h.
Gọi vận tốc xe chậm và xe nhanh lần lượt là x km/h và y km/h(x,y>0)
=>Độ dài quãng đường AB:5x+5y=400(km)
Nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
=>Thời gian xe chậm đi là 5h22p=\(\dfrac{161}{30}h\)
Thời gian xe nhanh đi là:5h22p-40p=4h42p=\(\dfrac{47}{10}h\)
=>Độ dài quãng đường AB là:\(\dfrac{161}{30}x+\dfrac{47}{10}y=400\)(km)
Theo bài ra ta có hệ PT:
\(\left\{{}\begin{matrix}5x+5y=400\\\dfrac{161}{30}x+\dfrac{47}{10}y=400\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x+y=80\\161x+141y=12000\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=36\\y=44\end{matrix}\right.\)
Vậy...
\(40p=\dfrac{2}{3}h;5h22'=\dfrac{161}{30}h\)
Gọi vận tốc xe thứ nhất là x(km/h), vận tốc xe thứ hai là y(km/h)
(Điều kiện: x>0 và y>0)
Hai xe nếu khởi hành cùng lúc thì sẽ gặp nhau sau 5h nên độ dài quãng đường hai xe đi được sẽ là:
5x+5y=400
=>5(x+y)=400
=>\(x+y=\dfrac{400}{5}=80\)
Thời gian xe thứ hai đi từ lúc khởi hành đến chỗ gặp nhau là \(5h22'=\dfrac{161}{30}\left(h\right)\)
Thời gian xe thứ nhất đi từ lúc khởi hành đến chỗ gặp nhau là \(\dfrac{161}{30}-\dfrac{2}{3}=\dfrac{161-20}{30}=\dfrac{141}{30}\left(h\right)\)
Độ dài quãng đường xe thứ nhất đi từ lúc khởi hành đến chỗ gặp là: \(\dfrac{141}{30}x\left(km\right)\)
Độ dài quãng đường xe thứ hai đi từ lúc khởi hành đến chỗ gặp là \(\dfrac{161}{30}y\left(km\right)\)
Tổng độ dài quãng đường hai xe đi được là 400km nên ta có: \(\dfrac{141}{30}x+\dfrac{161}{30}y=400\)
Do đó, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=80\\\dfrac{141}{30}x+\dfrac{161}{30}y=400\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=80\\141x+161y=400\cdot30=12000\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}141x+141y=11280\\141x+161y=12000\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-20y=-720\\x+y=80\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=36\\x=44\end{matrix}\right.\left(nhận\right)\)
Vậy: vận tốc xe thứ nhất là 44km/h
vận tốc xe thứ hai là 36km/h