Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Với giả thiết l << L và L << d thì ta có thể coi bài toán giống như giao thoa sóng ánh sáng với:
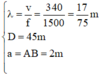
+ Khoảng cách hai điểm gần nhau nhất mà nghe thấy âm nhỏ nhất tương ứng với 1 khoảng vân nên:
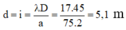
Đáp án C

Đáp án B
+ Bước sóng của sóng λ = v f = 0 , 8 m
+ Để tại N không nghe được âm thì N thuộc dãy cực tiểu
+ Ta có
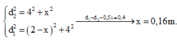
MN=1-0,16=0,84m
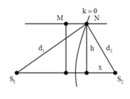

Đáp án D
S 1 M - S 2 M = k + 1 2 λ → 0 , 75 = k + 1 2 340 , 5 f → f = k + 1 2 340 , 5 0 , 75 f m i n ⇔ k = 0 → f m i n = 227 H

Đáp án B
+ Mức cường độ âm tại điểm M là trung điểm của AB được xác định bởi:
L M = 10 log P I 0 4 π S M 2 ↔ log P 10 - 12 4 π . 70 2 → P = 6 , 2 . 10 - 4 W.
→ Năng lượng giới hạn bởi hai mặt cầu E = P t = P A B v = 6 , 2 . 10 - 4 100 340 = 1 , 81 . 10 - 4 J.

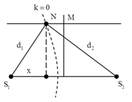

+ Ta có:
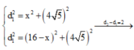

Kết hợp với chưc năng Shift → Slove của Casio, ta tìm được
M N m i n = 8 - x = 1,51 cm

Số âm nghe to nhất chính là số điểm dao động cực đại thỏa mãn:\(-AB < k\lambda < AB \Rightarrow \frac{-AB}{\lambda} < k < \frac{AB}{\lambda} \Rightarrow -10< k <10 \\ \Rightarrow k = -9,-8,\ldots,0,1,\ldots,9.\)
có 19 âm nghe to nhất.
Tương tự, số âm nghe nhỏ nhất là số điểm dao động cực tiểu thỏa mãn: \(-AB < (k+0.5)\lambda < AB \Rightarrow \frac{-AB}{\lambda} < k+0.5 < \frac{AB}{\lambda} \Rightarrow -10.5< k <9.5 \\ \Rightarrow k = -10,-8,\ldots,0,1,\ldots,9.\)
Có 20 âm nghe nhỏ nhất.

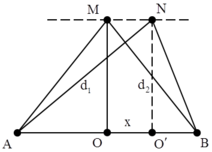

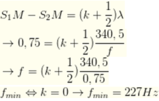
- Với giả thiết λ << L và L << d thì ta có thể coi bài toán giống như giao thoa sóng ánh sáng với:
- Khoảng cách hai điểm gần nhau nhất mà nghe thấy âm nhỏ nhất tương ứng với 1 khoảng vân nên: