K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

23 tháng 9 2021
tỉ lệ T1/T2=4/3=> k1/k2= 9/16=> song song k=k1+k1=9/16+1=25/16=> T ss/T2=4/5=0,48s

1 tháng 7 2016
\(T_1=2\pi\sqrt{\dfrac{m}{k_1}}\Rightarrow \dfrac{1}{k_1}=\frac{{T_1}^{2}}{{(2\pi)}^{2}m}\)
\(T_2=2\pi\sqrt{\dfrac{m}{k_2}}\Rightarrow \frac{1}{k_2}=\frac{{T_2}^{2}}{{(2\pi)}^{2}m}\)
Mắc nối tiếp 2 lò xo thì ta có: \(\dfrac{1}{k}=\dfrac{1}{k_1}+\dfrac{1}{k_2}=\frac{{T_1}^{2}}{{(2\pi)}^{2}m}+\frac{{T_2}^{2}}{{(2\pi)}^{2}m}=\frac{1}{{(2\pi)}^{2}m}(T_1^2+T_2^2)\)
Thay vào biểu thức
\(T=2\pi\sqrt{\dfrac{m'}{k}} =\sqrt{\dfrac{m'}{m}.(T_1^2+T_2^2)}\)
\(\Rightarrow \dfrac{0,3+0,4}{2}=0,5.\sqrt{\dfrac{m'}{m}}\)
\(\Rightarrow \dfrac{m'}{m}=0,49\)
\( \Rightarrow m'=0,49.m=0,49.200=98g \)



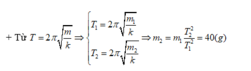

Chu kì: \(T=2\pi\sqrt{\dfrac{m}{k}}\)
\(\Rightarrow T^2\) tỉ lệ với \(\dfrac{1}{k}\), ta đặt \(T^2=\dfrac{a}{k}\)
Lò xo l1 thì: \(T_1^2=\dfrac{a}{k_1}\) (1)
Lò xo l2 thì: \(T_2^2=\dfrac{a}{k_2}\) (2)
Theo đề bài ta có 2 lò xo mắc song song: \(k=k_1+k_2\)
\(T^2=\dfrac{a}{k}\) (3)
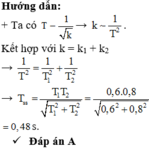
Từ (1), (2) và (3) ta suy ra: \(\dfrac{1}{T^2}=\dfrac{1}{T_1^2}+\dfrac{1}{T_2^2}\)
Đến đây bạn tính tiếp nhé.