Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đường tròn tâm B có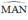 
là góc nội tiếp chắn cung 
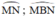là góc ở tâm chắn cung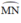 
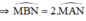
Đường tròn tâm C có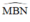 
là góc nội tiếp chắn cung 
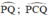là góc ở tâm chắn cung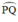 
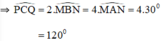
a) Đường tròn tâm B có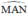 
là góc nội tiếp chắn cung 
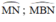là góc ở tâm chắn cung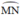 
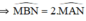
Đường tròn tâm C có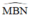 
là góc nội tiếp chắn cung 
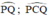là góc ở tâm chắn cung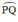 
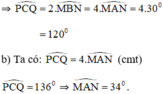
Kiến thức áp dụng
Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
a: ΔOBC cân tại O có OI là trung tuyến
nên OI vuông góc BC
góc AMO=góc ANO=góc AIO=90 độ
=>A,M,O,I,N cùng thuộc 1 đường tròn
b: Xét (O) có
AM,AN là tiếp tuyến
=>AM=AN
mà OM=ON
nên OA là trung trực của MN
=>OA vuông góc MN tại H
=>AH*AO=AM^2
Xét ΔAMB và ΔACM có
góc AMB=góc ACM
góc MAB chung
=>ΔAMB đồng dạng với ΔACM
=>AM/AC=AB/AM
=>AM^2=AB*AC=AH*AO
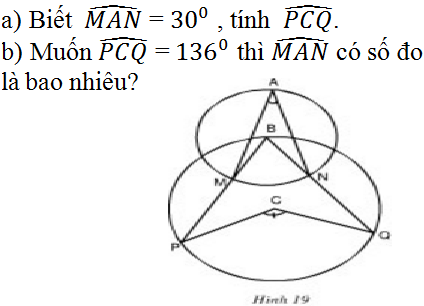
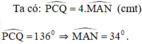
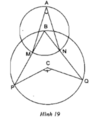
a)Ta có: \(\widehat{MAN}\)=\(\frac{1}{2}\)sđcung MN(góc nội tiếp chắn cung MN)
và \(\widehat{MBN}\)=sđcung MN (góc ở tâm chắn cung MN)
\(\Rightarrow\)\(\widehat{MAN}=\frac{1}{2}\)\(\widehat{MBN}\)=30
=>\(\widehat{MBN}\)=60
Ta lại có:\(\widehat{MBN}=\frac{1}{2}\)sđ cung PQ(góc nội tiếp chắn cung PQ)
và \(\widehat{PCQ}\)= sđ cung PQ(góc ở tâm chắn cung PQ)
=> \(\widehat{MBN}=\frac{1}{2}\widehat{PCQ}\)=60
=>\(\widehat{PCQ}\)= 120
b) Ta có:\(\widehat{MBN}=\frac{1}{2}\widehat{PCQ}\)(cmt)
mà \(\widehat{PCQ}\)=136 (gt)
=>\(\widehat{MBN}\)=68
mà \(\widehat{MAN}=\frac{1}{2}\widehat{MBN}\) (cmt)
=>\(\widehat{MAN}\)=34