Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) AOC^ + AOD^ = 180o (kề bù)
4* AOD^ + AOD^ = 180o
5* AOD^ = 180o
AOD^ = 36o => AOC^ = 144o
AOD^ = BOC^ = 36o (đđ)
AOC^ = BOD^ = 144o (đđ)
b) COM^ = DON^ (đđ) ; BOM^ = AON^ (đđ); COM^ = BOM^ => DON^ = AON^
c) AON^ = AOD^ /2 = 36o/2 = 18o
CON^ = AOC^ + AON^ = 144o + 18o = = 162o
=> ON ko vuông góc OC.


Tớ k vẽ hình , cậu tự vẽ nha!
Vì góc AOC+góc AOD =180 độ ( 2 góc kề bù)
mà góc AOC- góc AOD =20 độ
=> Góc AOC= (180độ + 20 độ ):2 =100 độ
Vì góc AOC và góc BOD là 2 góc đối đỉnh nên góc AOC= góc BOD = 100 độ.
=> góc AOD = 180 độ - 100 độ = 80 độ
=.> Góc AOD = GÓC BOC( 2 góc đối đỉnh)= 80 độ
Vậy=..

Có \(\widehat{AOC}\)và \(\widehat{AOD}\)cùng nằm trên CD
\(\Rightarrow\widehat{AOC}+\widehat{AOD}=180^0\)
Mà \(\widehat{AOC}-\widehat{AOD}=20^0\)
\(\Rightarrow\widehat{AOC}=\left(180^0+20^0\right):2\)
\(\Rightarrow\widehat{AOC}=100^0\)
\(\Rightarrow\widehat{AOD}=80^0\)
Vì CD cắt với AB tại O (GT)
\(\Rightarrow\widehat{AOC}\)và \(\widehat{BOD}\)là 2 góc đối đỉnh \(\Rightarrow\widehat{AOC}=\widehat{BOD}=100^0\)
\(\Rightarrow\widehat{AOD}\)và \(\widehat{COB}\)là 2 góc đối đỉnh \(\Rightarrow\widehat{AOD}=\widehat{COB}=80^0\)

ta có góc AOC+ góc AOD=180 độ (kề bù)
mà góc AOC - góc AOD=20 độ
\(\Rightarrow AOC=\left(180+20\right):2=100độ\)
\(\Rightarrow AOD=100-20=80độ\)
ta có : góc COB = góc AOD ( đối đỉnh) \(\Rightarrow COB=80độ\)
góc BOD = góc AOC ( đối đỉnh ) \(\Rightarrow BOD=100độ\)

Hình vẽ:
Giải:
Vì AB và CD cắt nhau tại O
Nên \(\widehat{AOC}\) và \(\widehat{AOD}\) là hai góc kề bù
\(\Leftrightarrow\widehat{AOC}+\widehat{AOD}=180^0\)
Mà theo đề bài thì \(\widehat{AOC}-\widehat{AOD}=20^0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{AOC}=\dfrac{180^0+20^0}{2}\\\widehat{AOD}=\dfrac{180^0-20^0}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{AOC}=100^0\\\widehat{AOD}=80^0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{BOD}=\widehat{AOC}\\\widehat{COB}=\widehat{AOD}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{BOD}=100^0\\\widehat{COB}=80^0\end{matrix}\right.\) (Các góc đối dỉnh)
Vậy \(\widehat{AOC}=100^0;\widehat{COB}=80^0;\widehat{BOD}=100^0;\widehat{DOA}=80^0\).
Chúc bạn học tốt!!!
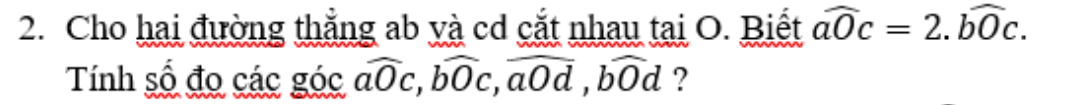
mik xin hình đc ko ?