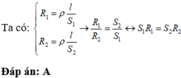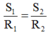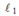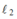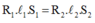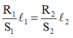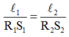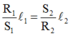Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Vì điện trở của các dây dẫn có cùng chiều dài và được làm từ cùng một loại vật liệu thì tỉ lệ nghịch với tiết diện của dây. Ta có: S 1 / S 2 = R 2 / R 1 ↔ S 1 R 1 = S 2 R 2

Điện trở tỷ lệ nghịch với tiết diện của dây 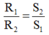
Hệ thức đúng là S1R1 = S2R2
→ Đáp án A

Đáp án A
Điện trở tỉ lệ nghịch với tiết diện nên R 1 / R 2 = S 2 / S 1 = > S 1 R 1 = S 2 R 2

Ta có: \(R_1=\rho\cdot\dfrac{l}{S}=2\Omega\)
\(R_2=\rho\cdot\dfrac{l_2}{S_2}=\rho\dfrac{3l_1}{\dfrac{S_1}{4}}=12R_1=12\cdot2=24\Omega\)
Chọn D.

Hai dây dẫn cùng chiều dài và cùng \(\rho\) nên ta có:
\(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}=\dfrac{1}{3}\)
\(\Rightarrow R_1=\dfrac{1}{3}R_2\)

Dây thứ nhất có: R 1 , l 1 , S 1
Dây thứ hai có: R 2 , l 2 , S 2
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 2 nhưng lại có tiết diện S 3 = S 1
Như vậy dây 1 và dây 3 có cùng vật liệu và tiết diện nhưng khác chiều dài.
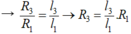
Lại có dây 2 và dây 3 có cùng vật liệu, cùng chiều dài, khác tiết diện.
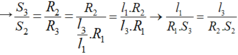
Thay
S
3
=
S
1
,
l
3
=
l
2
→ 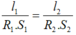 → Chọn D
→ Chọn D

Điện trở dây thứ nhất: \(R_1=\rho\cdot\dfrac{l_1}{S_1}=8\Omega\)
Điện trở dây thứ 2: \(R_2=\rho\cdot\dfrac{l_2}{S_2}=\rho\cdot\dfrac{l_1}{2}:2S_1=\rho\cdot\dfrac{l_1}{4S_1}=\dfrac{1}{4}R_1\)
\(\Rightarrow R_2=\dfrac{1}{4}\cdot8=2\Omega\)

Điện trở dây thứ nhất: \(R_1=p.\dfrac{l1}{S1}=8\)Ω
Điện trở dây thứ2: \(R_2=p.\dfrac{l2}{S2}=p.\dfrac{l1}{2}:2S1=p.\dfrac{l1}{4S1}=\dfrac{1}{4}R_1\)
⇒R2=\(\dfrac{1}{4}\)⋅8=2Ω
Ta có 2 dây dẫn được làm từ cùng một chất
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{\dfrac{l_1}{S_1}}{\dfrac{l_2}{S_2}}\)\(\Rightarrow\dfrac{8}{R_2}=\dfrac{\dfrac{2l_2}{S_1}}{\dfrac{l_2}{2S_1}}=\dfrac{2l_2}{S_1}.\dfrac{2S_1}{l_2}=4\)
\(\Rightarrow R_2=\dfrac{8}{4}=2\left(\Omega\right)\)