Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\hept{\begin{cases}\\\end{cases}}^2\theta^2\orbr{\begin{cases}\\\end{cases}}\sqrt{ }ℕ^∗\Delta\)

Gọi chân hải đăng là A thì ta để ý thấy. Lần đầu quan sát thì tam giác DAB là nửa tam giác đều
\(\Rightarrow DA^2+AB^2=DB^2\)
\(\Leftrightarrow DA^2+AB^2=4AB^2\)
\(\Leftrightarrow DA^2=3AB^2=3.75^2=11250\)
\(\Leftrightarrow DA=106,066\)
Lần thứ 2 quan sát thì tam giác CAB là tam giác vuông cân
\(\Rightarrow CA=AB=75\)
Vậy quãng đường thuyền đi được là:
\(DC=DA-CA=106,066-75=31,066\)

Đáp án:
Giải thích các bước giải:
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD – CK = CD – EF = 2 – 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9
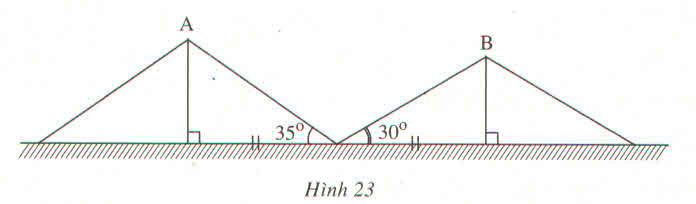
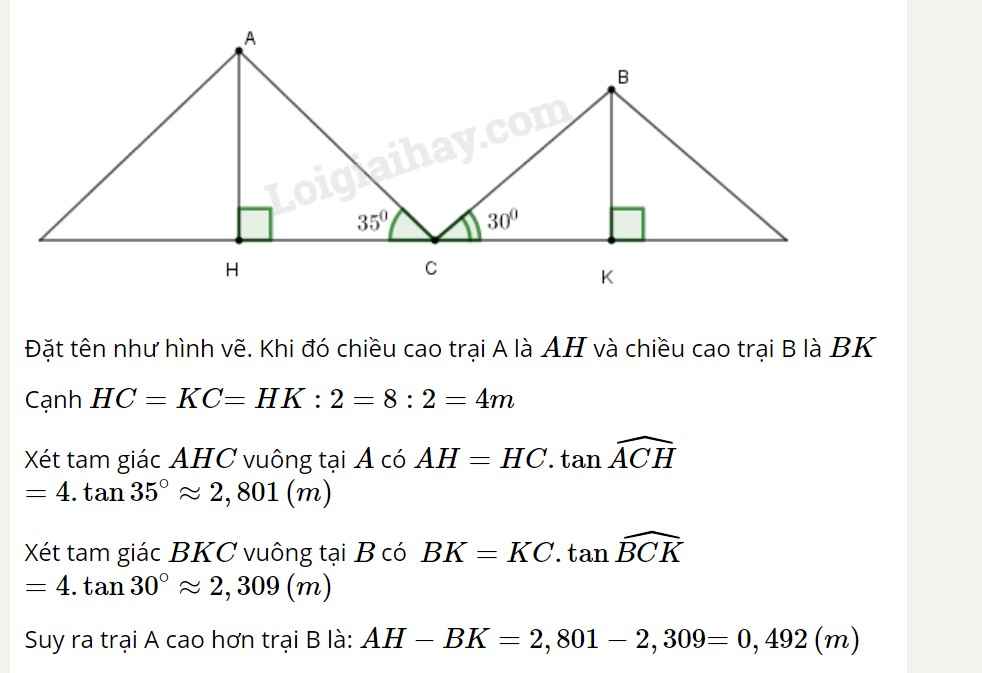
Chiều cao trại A là cạnh góc vuông đối diện với góc nhọn 35 ° , chiều cao trại B là cạnh góc vuông đối diện với góc nhọn 30 ° , cạnh kề với hai góc nhọn bằng nhau bằng 4m.
Chiều cao trại A là: 4.tg 35 ° ≈ 2,801 (m)
Chiều cao trại B là: 4.tg 30 ° ≈ 2,309 (m)
Trại A cao hơn trại B là: 2,801 – 2,309 = 0,492 (m)