Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

m(x – 4) = 5x – 2 ⇔(m - 5)x = 4m - 2
Nếu m - 5 ≠ 0 ⇔ m ≠ 5 thì phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Nếu m – 5 = 0 ⇔ m = 5, phương trình trở thành:
0.x = 18 ⇒ phương trình vô nghiệm
Vậy với m ≠ 5 phương trình có nghiệm duy nhất
x = (4m - 2)/(m - 5)
Với m = 5 phương trình vô nghiệm.

\(PT\Leftrightarrow m^2x-m^2-5mx+m+6x+2=0\\ \Leftrightarrow x\left(m^2-5m+6\right)=m^2-m-2\\ \Leftrightarrow x\left(m-2\right)\left(m-3\right)=\left(m-2\right)\left(m+1\right)\)
Với \(m\ne2;m\ne3\)
\(PT\Leftrightarrow x=\dfrac{\left(m-2\right)\left(m+1\right)}{\left(m-2\right)\left(m-3\right)}=\dfrac{m+1}{m-3}\)
Với \(m=2\Leftrightarrow0x=0\left(vsn\right)\)
Với \(m=3\Leftrightarrow0x=4\left(vn\right)\)
Vậy với \(m\ne2;m\ne3\) thì PT có nghiệm duy nhất \(x=\dfrac{m+1}{m-3}\), với \(m=2\) thì PT có vô số nghiệm và với \(m=3\) thì PT vô nghiệm

![]()
Phương trình (1) ⇔ x = -3m + 2
Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3
Vậy với mọi giá trị của m phương trình có nghiệm là:
x 1 = -3m + 2 và x 2 = (m - 2) / 3

m(x – 2) = 3x + 1
⇔ mx – 2m = 3x + 1
⇔ mx – 3x = 1 + 2m
⇔ (m – 3).x = 1 + 2m (1)
+ Xét m – 3 ≠ 0 ⇔ m ≠ 3, phương trình (1) có nghiệm duy nhất 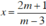
+ Xét m – 3 = 0 ⇔ m = 3, pt (1) ⇔ 0x = 7. Phương trình vô nghiệm.
Kết luận:
+ với m = 3, phương trình vô nghiệm
+ với m ≠ 3, phương trình có nghiệm duy nhất 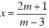

m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
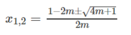

Phương trình đã cho tương đương với phương trình
(m - 1)(m + 3)x = 4(m - 1)
Với m ≠ 1 và m ≠ -3 phương trình có nghiệm ![]()
Với m = 1 mọi số thực x đều là nghiệm của phương trình;
Với m = -3 phương trình vô nghiệm.

Với ![]() phương trình đã cho trở thành
phương trình đã cho trở thành
3x + 2m = x - m ⇔ 2x = -3m ⇔ x = -3m / 2
Ta có:
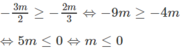
Với ![]() Phương trình đã cho trở thành
Phương trình đã cho trở thành
-3x - 2m = x - m ⇔ 4x = -m ⇔ x = -m / 4
Ta có:
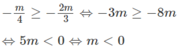
Kết luận
Với m > 0 phương trình vô nghiệm;
Với m = 0 phương trình có nghiệm x = 0;
Với m < 0 phương trình có nghiệm
![]()

Điều kiện của bất phương trình là x ≥ 0
Nếu m ≤ 1 thì m - 1 ≤ 0, bất phương trình đã cho nghiệm đúng với mọi x ≥ 0
Nếu m > 1 thì m – 1 > 0, bất phương trình đã cho tương đương với √x ≤ 0 ⇔ x = 0
Vậy: Nếu m ≤ 1 thì tập nghiệm của bất phương trình là [0; +∞)
Nếu m > 1 thì tập nghiệm của bất phương trình là {0}

(2m + 1)x – 2m = 3x – 2
⇔ (2m + 1)x – 3x = 2m – 2
⇔ (2m + 1 – 3).x = 2m – 2
⇔ (2m – 2).x = 2m – 2 (3)
+ Xét 2m – 2 ≠ 0 ⇔ m ≠ 1, pt (3) có nghiệm duy nhất 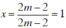
+ Xét 2m – 2 = 0 ⇔ m = 1, pt (3) ⇔ 0.x = 0, phương trình có vô số nghiệm.
Kết luận :
+ Với m = 1, phương trình có vô số nghiệm
+ Với m ≠ 1, phương trình có nghiệm duy nhất x = 1.
Giải và biện luận phương trình sau theo tham số m: m(x – 4) = 5x – 2.
\(m\left(x-4\right)=5x-2\\ \Rightarrow mx-4x=5x-2\\\Rightarrow mx-5x=4x-2\\ \Rightarrow x\left(m-5\right)=4x-2 \)
Trong trường hợp phương trình có nghiệm duy nhất thì
\(m-5\ne0\\ \Rightarrow m\ne5\)=> \(x=\frac{4m-2}{m-5}\)
Còn trong trường hợp m - 5 = 0 <=> m = 5 thì
\(x=\frac{20-2}{5-5}=>0.x=18\)
=> Phương trình vô nghiệm
Vậy ta có kết luận
Phương trình có nghiệm duy nhất khi \(m\ne5\)
Phương trình vô nghiệm khi m = 5
TL:
ko bt thì đùng nói để mk
cho ẩn nh=ghen