Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1
Đáp án B
Ta có tập xác định D = ℝ và y ' = 4 + m + 1 cosx − msinx
Hàm số đồng biến trên ℝ ⇔ y ' ≥ 0 , ∀ x ∈ D ⇔ Min ℝ 4 + m + 1 cosx − msinx ≥ 0
Ta có
m + 1 cosx − msinx ≥ − 2 m 2 + 2 m + 1 , ∀ x
⇒ 4 + m + 1 cosx − msinx ≥ 4 − 2 m 2 + 2 m + 1 , ∀ x
⇒ Min ℝ 4 + m + 1 cosx − msinx = 4 − 2 m 2 + 2 m + 1 ≥ 0
⇔ 2 m 2 + 2 m − 15 ≤ 0 ⇔ − 1 − 31 2 ≤ m ≤ − 1 + 31 2
Do m ∈ ℤ ⇒ m ∈ S = − 3 ; − 2 ; − 1 ; 0 ; 1 ; 2 . Vậy S có 6 phần tử
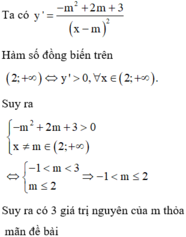
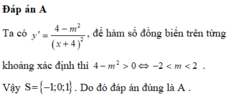
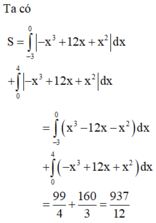
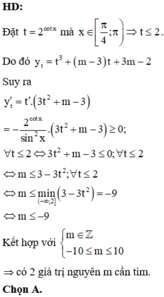
Đáp án A