Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

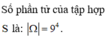
Gọi là biến cố: Chọn được 1 số chia hết cho 6 từ tập hợp S”
Số chia hết cho 6 có dạng: 


Đáp án D
Ta thu được số chẵn khi chữ số hàng đơn vị là chắn. Do vai trò của 7 số trong đó có 3 số chẵn là như nhau nên xác suất cần tính bằng 3 7

Tập S có 9 4 phần tử. Ta có
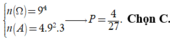
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
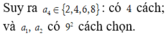
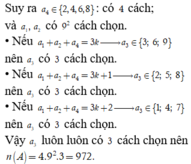

Đáp án A
Gọi số cần tìm có dạng a b c d ¯ vì a b c d ¯ chia hết cho 6 ⇒ d = { 2 ; 4 ; 6 ; 8 } a + b + c + d : 3 .
Khi đó, chọn d có 4 cách chọn; b và c đều có 9 cách chọn (từ 1 → 9 )
Nếu b + c + d:3 thì a = {3;6;9} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 1 thì a = {2;5;8} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 2 thì a = {1;4;7} ⇒ có 3 cách chọn a
Suy ra a chỉ có 3 cách chọn ⇒ có 4.9.9.3 = 972 số chia hết cho 6
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .

Đáp án A.
Gọi số cần tìm có dạng
a
b
c
d
vì chia hết cho 6 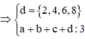
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1→9).
· Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
· Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
· Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là ![]()

ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....




Đáp án D