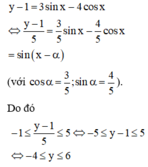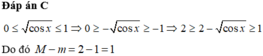Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: y = cos x + 2 sin x + 3 2 cos x − sin x + 4
⇒ y 2 cos x − sin x + 4 = cos x + 2 sin x + 3
⇔ 2 + y sin x + 1 − 2 y cos x = 4 y − 3 1
PT (1) có nghiệm ⇔ 2 + y 2 + 1 − 2 y 2 ≥ 4 y − 3 2
⇔ 11 y 2 − 24 y + 4 ≤ 0 ⇔ 2 11 ≤ y ≤ 2
Suy ra M = 2 m = 2 11 ⇒ M . m = 4 11

Chọn B
Vì sinx-cosx+3>0 nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình (1-y)sinx+(y+1)cosx=(1+3y) có nghiệm.
Sử dụng điều kiện có nghiệm của phương trình A.sinx+B.cosx=C. Vậy m = -1 và M=1/7

Đáp án D.
Phương pháp
Sử dụng tập giá trị của hàm y = sin x : 1 ≤ sin x ≤ 1 để đánh giá hàm số bài cho
Cách giải
Ta có:
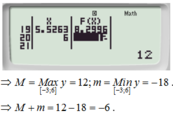
− 1 ≤ s i n x ≤ 1 ⇒ − 1 ≤ − s i n x ≤ 1
2 − 1 ≤ 2 − s i n x ≤ 2 + 1 ⇔ 1 ≤ 2 − s i n x ≤ 3 ⇒ M = 3 ; m = 1

Đáp án C.
Ta có: f 2 x = 2 + sin x + cos x + 2 1 + sin x 1 + c o s x
= 2 + sin x + cos x + 2 1 + sin x + cos x + sin x cos x
Đặt t = sin x + cos x = 2 sin x + π 4 ⇒ t ∈ - 2 ; 2 .
Suy ra sin x cos x = t 2 - 1 2 ⇒ f 2 x = 2 + t + 2 1 + t + t 2 - 1 2 = 2 + t + 2 t 2 + 2 t + 1
⇒ f t = t + 2 + 2 t + 1 = t + 2 + 2 t + 1 k h i t ≥ - 1 t + 2 - 2 t + 1 k h i t < - 1 = 1 + 2 t + 2 + 2 k h i t ≥ - 1 1 - 2 t + 2 - 2 k h i t < - 1
Từ đó suy ra 1 ≤ f 2 x ≤ 4 + 2 2 ⇔ f x ≤ 4 + 2 2 ⇒ M - m = 4 + 2 2 - 1 .