Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Mực nước trong bồn sau khi bơm được 56 giây là: ∫ 0 56 h ' t d t = ∫ 0 56 1 5 . t + 8 d t = 36 (cm)

Đáp án C.
Mức nước ở bồn sau khi bơm được tính bằng công thức ∫ 0 56 1 5 t + 8 3 d t .
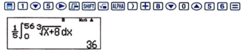
Sau khi bơm được 56 giây thì mức nước trong bồn là 36 cm. Ta chọn C.

Mức nước ở bồn sau khi bơm nước được 6 giây:
h 6 = ∫ 0 6 h ' t d t = 3 20 t + 8 4 3 - 12 5 ≈ 2 , 66 c m
Đáp án B

Ta có
∫ 0 5 3 a t 2 + b t d t = a t 3 + 1 2 b t 2 0 5 = 125 a + 25 2 b = 150
Tương tự ta có 1000a + 50b = 1100
Vậy từ đó ta tính được a = 1; b = 2
Vậy thể tích nước sau khi bơm được 20 giây là :
∫ 0 20 h ' t d t = t 3 + t 2 0 20 = 8400 m 3
Đáp án A

Đáp án B.
Ta có h ( t ) = ∫ h ' ( t ) d t = 3 2000 ( t + 3 ) 4 3 + C
Lúc ban đầu t = 0 hồ bơi không có nước tức là:
h ( t ) = 0 ⇔ 3 2000 0 + 3 4 3 + C = 0 ⇔ C = - 3 7 3 2000
⇒ Mực nước bơm tại thời điểm t là: h ( t ) = 3 2000 ( t + 3 ) 4 3 - 3 7 3 2000
Theo giả thiết ⇒ h ( t ) = 3 4 . 280 ⇔ 3 2000 t + 3 4 3 - 3 7 3 2000 = 210
⇔ t + 3 4 3 = 140004 , 33 ⇔ t = 7232 ( s ) ⇒ t = 2 giờ 34 giây.

Đáp án B
Yêu cầu bài toán “Tìm R để diện tích toàn phần của hình truh là nhỏ nhất”
Gọi h là chiều cao của hình trụ Thể tích khối trụ là V = π R 2 h = 10 ⇒ h = 10 π R 2 1
Diện tích toàn phần của hình trụ là: S T P = S x q + 2 × S d = 2 π R h + 2 π R 2 2
Từ (1); (2) suy ra S T P = 2 π R 2 + 20 R = 2 π R 2 + 10 R + 10 R ≥ 3 200 π 3
Dấu = xảy ra khi và chỉ khi 2 π R 2 = 10 R ⇔ R = 5 π 3 m

Đáp án B.
Gọi h(m) là chiều cao của chiếc bồn nước, h > 0 .
Thể tích của chiếc bồn là V = π r 2 h = 10 ⇒ h = 10 π r 2 .
Diện tích toàn phần của chiếc bồn là:
S t p = 2 π r 2 + 2 π r h = 2 π r 2 + 2 π r . 10 π r 2 = 2 π r 2 + 20 r = 2 π r 2 + 10 r + 10 r
Cách 1: Theo bất đẳng thức Côsi ta có: S t p ≥ 3 2 π r 2 . 10 r . 10 r 3 = 3. 200 π 3 .
Dấu “=” xảy ra khi
2 π r 2 = 10 r ⇔ r 3 = 5 π ⇔ r = 5 π 3
Vậy với r = 5 π 3 thì lượng inox được sử dụng để làm bồn nước là ít nhất.
Cách 2: Xét hàm số f r = 2 π r 2 + 20 r , r > 0 .
Ta có
f ' r = 4 π r − 20 r 2 = 4 π r 3 − 20 r 2 ; f ' r = 0 ⇔ 4 π r 3 − 20 = 0 ⇔ r 3 = 5 π ⇔ r = 5 π 3
Bảng biến thiên:
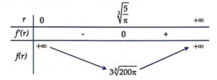
⇒ f r đạt giá trị nhỏ nhất tại r = 5 π 3 .


Đáp án C