Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương trình hoành độ giao điểm của (C) và d : x − 2 x − 1 = − x + m
⇔ x ≠ 1 x − 2 = ( − x + m ) ( x − 1 ) ⇔ x ≠ 1 f ( x ) = x 2 − m x + m − 2 = 0 ( * )
Để (C) và d cắt nhau tại hai điểm phân biệt A, B khi và chỉ khi phương trình (*) có hai nghiệm phân biệt x 1 , x 2 khác 1
⇔ f ( 1 ) = 1 2 − m + m − 2 ≠ 0 Δ = - m 2 − 4 ( m − 2 ) > 0 ⇔ − 1 ≠ 0 m 2 − 4 m + 8 m > 0 ⇔ m ∈ ℝ .
Mặt khác OAB là tam giác nên O ∈ d hay m ≠ 0 .
Gọi A ( x 1 ; − x 1 + m ) và B ( x 2 ; − x 2 + m ) . Suy ra O A = 2 x 1 2 − 2 m x 1 + m 2 O B = 2 x 2 2 − 2 m x 2 + m 2
Do x 1 , x 2 là hai nghiệm của phương trình (*) nên x 1 2 − m x 1 = 2 − m x 2 2 − m x 2 = 2 − m
Khi đó O A = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4 O B = 2 ( 2 − m ) + m 2 = m 2 − 2 m + 4
Từ giả thiết ta có :
2 m 2 − 2 m + 4 = 1 ⇔ m 2 − 2 m + 4 = 2 ⇔ m ( m − 2 ) = 0 ⇔ m = 0 m = 2
Đối chiếu với điều kiện ta được m=2 thỏa mãn.

Đáp án D
Xét pt tương giao:
x + 1 = 2 x + 4 x − 1 ⇔ ( x + 1 ) ( x − 1 ) = 2 x + 4 ⇔ x 2 − 2 x − 5 = 0 ⇔ x = 1 ± 6 ⇒ x I = 1

Đáp án D
Xét pt tương giao:
x + 1 = 2 x + 4 x − 1 ⇔ ( x + 1 ) ( x − 1 ) = 2 x + 4 ⇔ x 2 − 2 x − 5 = 0 ⇔ x = 1 ± 6 ⇒ x I = 1

Đáp án A
Ta có 3 x + y − 4 = 0 ⇔ y = 4 − 3 x
y 1 = − 2 y ' 1 = − 3 ⇔ 1 + b a − 2 = − 2 − 2 − a b a − 2 2 = − 3
⇔ b = 3 − 2 a − 2 − a 3 − 2 a = − 3 a 2 − 4 a + 4
⇔ b = 3 − 2 a a = 1 a = 2 ⇔ a = 1 b = 1 a = 2 b = − 1 L
Vậy a = 1 ; b = 1 ⇒ a + b = 2

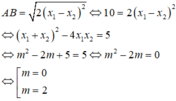





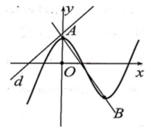
Chọn A.
Hoành độ A,B là nghiệm của pt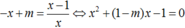
→ xA + xB = m – 1 = 1 ⇔ m = 2