
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{5\cdot4^{15}\cdot9^9-4\cdot3^{20}\cdot8^9}{5\cdot2^{29}\cdot9^{10}-7\cdot2^{29}\cdot27^6}\)
\(=\dfrac{5\cdot2^{30}\cdot3^{18}-2^2\cdot2^{27}\cdot3^{20}}{5\cdot2^{29}\cdot3^{20}-7\cdot2^{29}\cdot3^{18}}\)
\(=\dfrac{2^{29}\cdot3^{18}\left(5\cdot2-3^2\right)}{2^{29}\cdot3^{18}\left(5\cdot3^2-7\right)}\)
\(=\dfrac{10-9}{5\cdot9-7}=\dfrac{1}{38}\)

\(2^3+\left(\dfrac{1}{5}\right)^4+5^4=8+\dfrac{1}{625}+625=\dfrac{5000+1+625^2}{625}=\dfrac{395626}{625}\)
\(Sửa:2^3+\left(\dfrac{1}{5}\right)^4\cdot5^4=8+\left(\dfrac{1}{5}\cdot5\right)^4=8+1=9\)

b) (5/2-3x)=25/9
3x = 5/2-25/9
3x =-5/18
x =-5/18:3
x=-5/54
\(e.\left(x-1\right)^5=-32\)
\(\left(x-1\right)^5=\left(-2\right)^5\)
\(x-1=-2\)
\(x\) \(=-2+1\)
\(x\) \(=-1\)
Vậy \(x=-1\)

(x/2-3)5=32
<=>(x/2-3)5=25
<=>x/2-3=2
<=>x=(2+3).2
<=>x=10
!!!!!CHÚC!!MAY!!MẮN!!!!!

a, (-0,2)2 \(\times\) 5 - \(\dfrac{2^{13}\times27^3}{4^6\times9^5}\)
= 0,04 \(\times\) 5 - \(\dfrac{2^{13}\times3^9}{2^{12}\times3^{10}}\)
= 0,2 - \(\dfrac{2}{3}\)
= \(\dfrac{2}{10}\) - \(\dfrac{2}{3}\)
= - \(\dfrac{7}{15}\)
b, \(\dfrac{5^6+2^2.25^3+2^3.125^2}{26.5^6}\)
= \(\dfrac{5^6+4.5^6+8.5^6}{26.5^6}\)
= \(\dfrac{5^6.\left(1+4+8\right)}{26.5^6}\)
= \(\dfrac{1}{2}\)

3^x*5^x-1=224
3^x*5^x/5=224
15^x=224*5
15^x=1120
=>ko tồn tại x thỏa mãn đề bài vị 15^x luôn có tận cùng bằng 5 (x khác 0 ) hoặc 1 ( x=0) ma 1120 co tận cùng bằng 0

A = |\(x\) + 5| + 2023
|\(x\) + 5| ≥ 0 ⇒| \(x\) + 5| + 2023 ≥ 2023⇒ A(min) = 2023 xảy ra khi \(x\) = -5
B = (\(x+2\))2 - 2023
(\(x\) + 2)2 ≥ 0 ⇒ (\(x\) + 2)2 ≥ - 2023 ⇒ A(min) = -2023 xảy ra khi \(x\) = -2
C = \(x^2\) - 6\(x\) + 20
C = (\(x^2\) - 3\(x\)) - ( 3\(x\) - 9) + 11
C = \(x\)(\(x-3\)) - 3(\(x\) -3) + 11
C = (\(x-3\))(\(x\)-3) + 11
C = (\(x-3\))2 + 11
(\(x\) -3)2 ≥ 0 ⇒ (\(x\) - 3)2 + 11 ≥ 11 vậy C(min) = 11 xảy ra khi \(x=3\)
D = \(x^2\) + 10\(x\) - 25
D = \(x^2\) + 5\(x\) + 5\(x\) + 25 - 55
D = (\(x^2\) + 5\(x\)) + (5\(x\) + 25) - 50
D = \(x\)(\(x\) + 5) + 5(\(x\) + 5) - 50
D = (\(x\) +5)(\(x\) + 5) - 50
D = ( \(x\) + 5)2 - 50
(\(x+5\))2 ≥ 0 ⇒ (\(x\) + 5)2 - 50 ≥ -50 ⇒ D(min) = -50 xảy ra khi \(x\) = -5

Ta có:
2x=3y\(\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x^2}{9}=\frac{2y^2}{8}\)và x2+2y2=17
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x^2}{9}=\frac{2y^2}{8}=\frac{x^2+2y^2}{9+8}=\frac{17}{17}=1\)
Do đó: x2=9\(\Rightarrow\orbr{\begin{cases}x=-3\\x=3\end{cases}}\)
x2=4\(\Rightarrow\orbr{\begin{cases}x=-2\\x=2\end{cases}}\)
Vậy x=-3;y=-2 hoặc x=3;y=2
Ta có 2x=3y
=>\(\frac{x}{3}\)=\(\frac{y}{2}\)
Đặt \(\frac{x}{3}\)=\(\frac{y}{2}\)=k
=>x=3k ; y=2k
Mà x2+2y2=17
=> (3k)2+ 2(2k)2=17
<=> 9*k2+2*4*k2=17
<=> 9*k2+8*k2=17
<=> k2*(9+8) =17
<=> k2 *17=17
<=>k2=1
<=> k=1 hoặc k=-1
TH1.k=1
=> x=3*1=3; y=2*1=2
TH2. k=-1
=> x=3*(-1)=-3 ; y=2*(-1)=-2
Vậy x=3;y=2 hoặc x=-3 ; y=-2
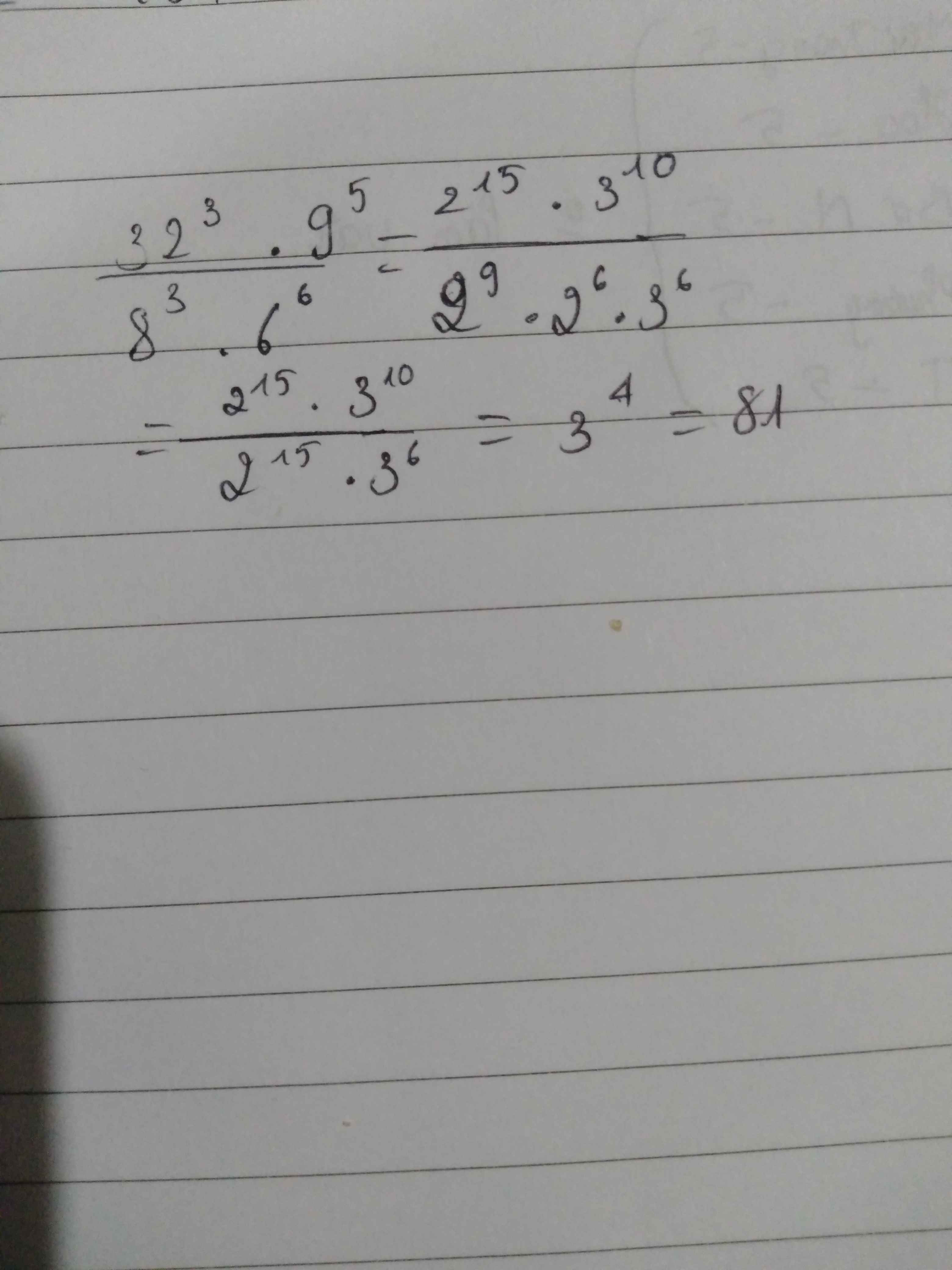
\(x^5=32^4\)
\(=>x^5=\left(2^5\right)^4=\left(2^4\right)^5\)
\(=>x=2^4=16\)
h cho mình nha!
x5 = 324
=> x5 = (25)4 = (24)5
=> x = 24 = 16