Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dựa vào biểu thức tính tốc độ giới hạn của xe chạy theo đường vòng cung, ta có tốc độ tối đa của xe để giữ an toàn tỉ lệ thuận với căn bậc 2 của hệ số ma sát nghỉ và bán kính đường tròn
Tốc độ này không phụ thuộc vào trọng lượng của xe.
=> Những yếu tố quan trọng cần lưu ý khi thiết kế cầu đường có hình vòng cung:
+ Mặt đường phải nghiêng một góc θ so với phương ngang để hợp lực hướng vào tâm đường tròn và đóng vai trò là lực hướng tâm.
Dựa vào biểu thức tính tốc độ giới hạn của xe chạy theo đường vòng cung, ta có tốc độ tối đa của xe để giữ an toàn tỉ lệ thuận với căn bậc 2 của hệ số ma sát nghỉ và bán kính đường tròn
Tốc độ này không phụ thuộc vào trọng lượng của xe.
=> Những yếu tố quan trọng cần lưu ý khi thiết kế cầu đường có hình vòng cung:
+ Mặt đường phải nghiêng một góc θ so với phương ngang để hợp lực hướng vào tâm đường tròn và đóng vai trò là lực hướng tâm.
1 phút = 60s
- Chu kì: T = \(\dfrac{t}{n}\)= \(\dfrac{60}{4}\)= 15 (s)
- Tần số: f = \(\dfrac{1}{T}\)=\(\dfrac{1}{15}\)(Hz)
- Tốc độ góc: T = \(\dfrac{2\pi}{\omega}\) \(\Rightarrow\) \(\omega=\dfrac{2\pi}{T}\)\(=\) \(\dfrac{2\pi}{15}=\dfrac{2}{15}\pi\) (rad/s)
- Tốc độ dài: \(\upsilon=r\omega\) ⇔ \(\upsilon=\dfrac{3}{2}.\dfrac{2}{15}\pi\) = \(\dfrac{1}{5}\pi\) (m/s)
- Gia tốc hướng tâm: \(a_{ht}=r.\omega^2\Leftrightarrow a_{ht}=\dfrac{3}{2}.\left(\dfrac{2}{15}\pi\right)^2\)\(\simeq\) 0,263 (m/\(s^2\))
vậy bài em làm như này sai òi hả🥲 cảm mơn
Gia tốc hướng tâm:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{30^2}{50}=18\)m/s2
Chọn A.
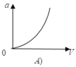
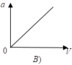
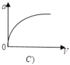
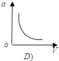
Gia tốc hướng tâm: a = an = v2/R
→ Đồ thị biểu diễn sự phụ thuộc của a theo R là một cung Parabol đồng biến.
Đáp án A.
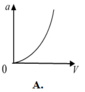
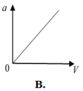
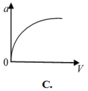
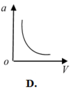
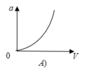
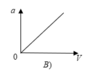
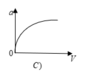
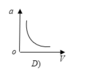
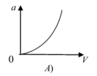
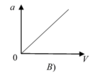
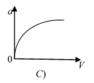
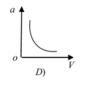
a = v 2 R nên đồ thị là 1 nhánh parabol theo v vì R = const
Đáp án A.
a = v 2 R nên đồ thị là 1 nhánh parabol theo v vì R = c o n s t
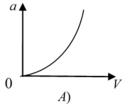
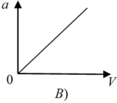
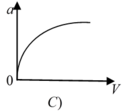
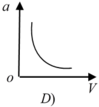
Ở các đoạn đường cong, người ta thường làm mặt đường nghiêng về phía tâm của đoạn cong để xe vẫn có thể đi với tốc độ lớn.
Em có thể xem giải thích chi tiết tại bài giảng của OLM nhé: https://www.youtube.com/watch?v=N8hulXWK-1Y