Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-OM cắt DC tại N'.
\(\dfrac{AM}{DN}=\dfrac{MB}{NC}=\dfrac{AM+MB}{DN+BC}=\dfrac{AB}{DC}\)
-Xét △ODN' có: AM//DN'.
\(\Rightarrow\dfrac{AM}{DN'}=\dfrac{OM}{MN'}\) (hệ quả định lí Ta-let) (1)
-Xét △OCN' có: BM//CN'.
\(\Rightarrow\dfrac{BM}{CN'}=\dfrac{OM}{MN'}\) (định lí Ta-let) (2)
-Từ (1) và (2) suy ra:
\(\dfrac{AM}{DN'}=\dfrac{BM}{CN'}=\dfrac{AM+BM}{CN'+DN'}=\dfrac{AB}{CD}\)
\(\Rightarrow\dfrac{AM}{CN'}=\dfrac{BM}{DN'}=\dfrac{AM}{CN}=\dfrac{BM}{DN}\)
\(\Rightarrow CN=CN';DN=DN'\)
\(\Rightarrow N\equiv N'\)
-Vậy MN đi qua điểm O.

Trả lời
Vì \(\hept{\begin{cases}AM=MB\\DC=NC\\MN=\frac{BC+AD}{2}\end{cases}}\Rightarrow MN\) là đường trung bình của hình thang
\(\Rightarrow ABCD\)là hình thang ( đpcm )
Thông cảm nha mọi người
tôi sẽ vẽ lại hình cho nha
Study well

a) Ta có: AB//CD(ABCD là hthang cân)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\widehat{ODC}\\\widehat{OBA}=\widehat{OCD}\end{matrix}\right.\)
Mà \(\widehat{ODC}=\widehat{OCD}\)(ABCD là hthang cân)
\(\Rightarrow\widehat{OBA}=\widehat{OAB}\)
=> Tam giác OAB cân tại O
b) Xét hthang ABCD có:
M là trung điểm AD(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> \(MN=\dfrac{AB+CD}{2}=\dfrac{6+10}{2}=8\left(cm\right)\)
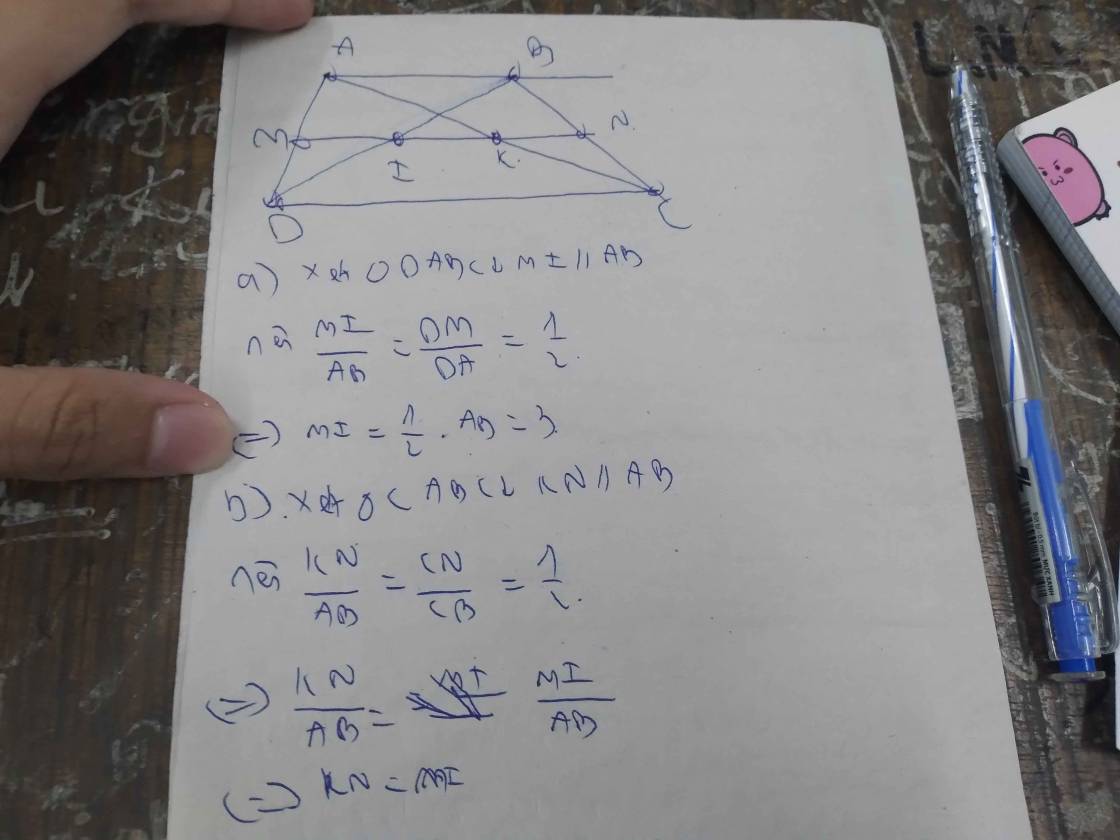
a)
Ta có:\(\frac{AM}{DM}\)=\(\frac{BN}{CN}\)(do cùng bằng 1)
Theo định lý Thales, ta suy ra MN//CD
Vậy:MN//AB,MN//CD do CD//AD
b)
Gọi E,F lần lượt là giao điểm của AB với DN và AN với CD
Ta có: AM=DM,MN//DF nên MN là đường trung bình của \(\Delta\)ADF
tương tự MN cũng là đường trung bình của \(\Delta\)ADE
Do đó AE+DF=MN
<=>AB+BE+CD+CF=MN
mà ta dễ dàng chứng minh được AB=CF và CD=BE
Cho nên: 2(AB+CD)=MN
Vậy: AB+CD=\(\frac{MN}{2}\)
1 là j vậy cảm ơn nhìu