
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Gọi chiều rộng ban đầu là x(m) x>0
Chiều dài ban đầu : x+10(m)
Chiều rộng sau khi được tăng: x+5(m)
Chiều dài sau khi giảm: x+10-2=x+8(m)
Theo bài ra ta có pt
(x+8)(x+5)-x(x+10)=100
Giải ra được x=20(m)
Chiều dài : 20=10=30(m)
Diện tích mảnh vườn:20.30=600(m\(^2\))
b, Gọi vận tốc trung bình của xe mày là x(km/h) x>0
Vận tốc tb của ô tô là : x+6(km/h)
Theo bài ra ta có pt
2x+2(x+6)=140
Giải ra được x=32(km/h)
Vtb của ô tô là 32+6=38(km/h)

Lời giải:
a.
\(G=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{(2x-3)(x+1)-(2x+1)(x-1)}{(x-1)(x+1)}\)
\(=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{-2}{(x-1)(x+1)}=\frac{x^2-4}{x+1}+\frac{2}{x+1}.\frac{(x+1)(x-1)}{-2}\)
\(=\frac{x^2-4}{x+1}-(x-1)=\frac{x^2-4-(x^2-1)}{x+1}=\frac{-3}{x+1}\)
b.
Để $A\in\mathbb{Z}^+$ thì $x+1$ là ước âm của $-3$
$\Rightarrow x+1\in\left\{-1;-3\right\}$
$\Leftrightarrow x\in\left\{-2;-4\right\}$ (tm)
c.
$G< -1\Leftrightarrow \frac{-3}{x+1}+1< 0$
$\Leftrightarrow \frac{x-2}{x+1}< 0$
$\Leftrightarrow x-2<0< x+1$ hoặc $x-2>0>x+1$
$\Leftrightarrow -1< x< 2$ (chọn) hoặc $-1> x>2$ (loại)
Vậy $-1< x< 2$ và $x\neq 1$
Bài 8:
a: Ta có: \(G=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\left(\dfrac{2x-3}{x-1}-\dfrac{2x+1}{x+1}\right)\)
\(=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\dfrac{2x^2+2x-3x-3-2x^2+2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{2}{x+1}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{-x+1}{1}\)
\(=\dfrac{x^2-4-\left(x-1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x^2-4-x^2+1}{x+1}\)
\(=-\dfrac{3}{x+1}\)

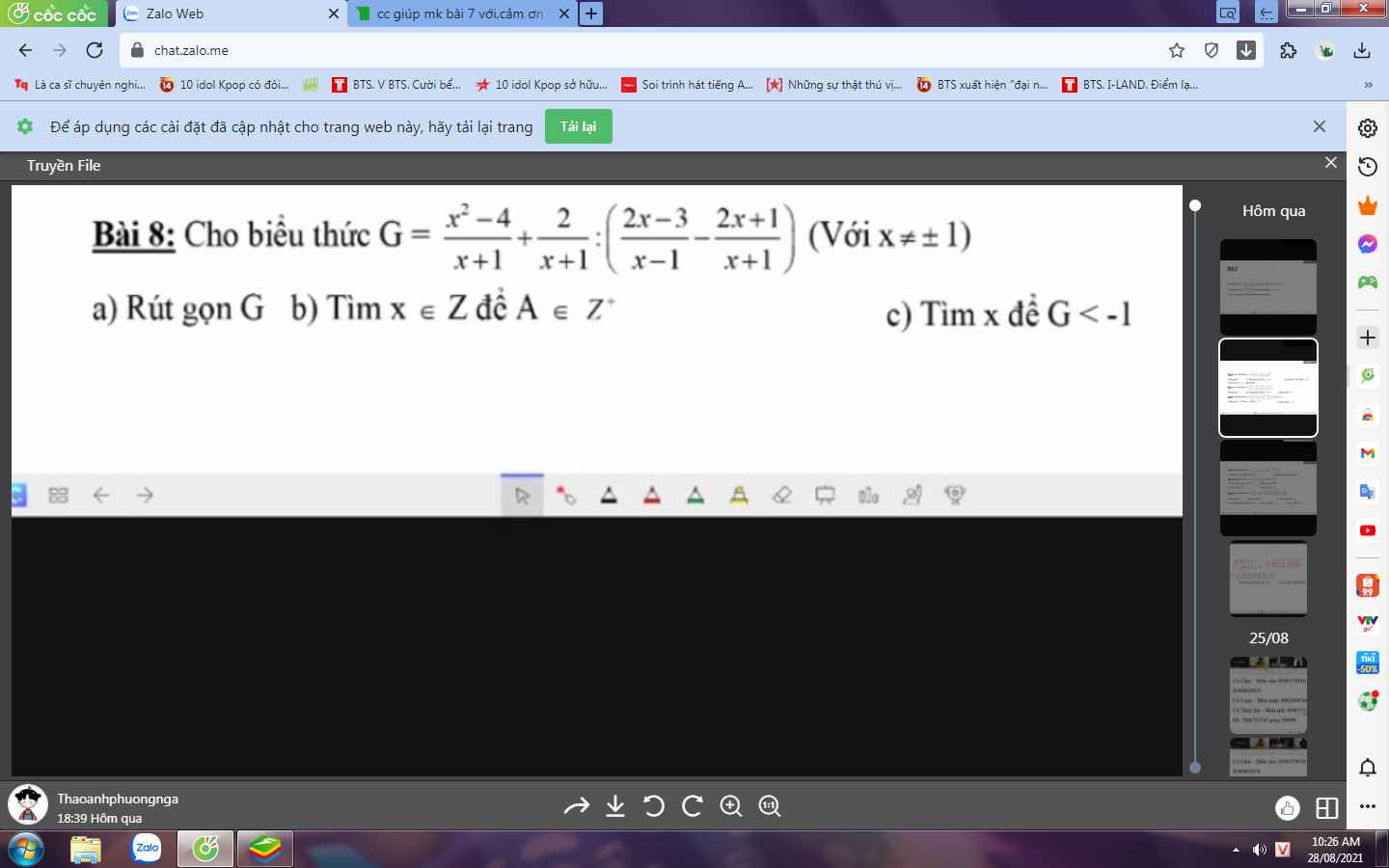
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)


c, là hằng đẳng thức nha bạn
(\(\sqrt{x}\)+\(\sqrt{2x}\))2=0
suy ra \(\sqrt{x}\)+\(\sqrt{2x}\)=0
\(\sqrt{x}\)=\(\sqrt{2x}\)
suy ra x=0
Bài 2: Tìm x:
a) \(3x^2\)\(-27x=0\)
\(< =>3x\left(x-9\right)=0\)
\(=>x=0\) hay \(x-9=0\)
\(=>x=0\) hay \(x=9\)

Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)

c) Ta có: \(P=2x+\dfrac{1}{x+1}\)
\(\Leftrightarrow\dfrac{-x}{x+1}=2x+\dfrac{1}{x+1}\)
\(\Leftrightarrow\dfrac{-x}{x+1}=\dfrac{2x\left(x+1\right)+1}{x+1}\)
Suy ra: \(2x^2+2x+1=-x\)
\(\Leftrightarrow2x^2+3x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\left(loại\right)\\x=-\dfrac{1}{2}\left(nhận\right)\end{matrix}\right.\)
Vậy: Để \(P=2x+\dfrac{1}{x+1}\) thì \(x=-\dfrac{1}{2}\)
`a)F=((x+1)/(1-x)-(1-x)/(x+1)-(4x^2)/(x^2-1)):(4x^2-4)/(x^2-2x+1)`
`đk:x ne +-1`
`F=((-(x+1)^2+(x-1)^2-4x^2)/(x^2-1)):(4(x-1)(x+1))/(x-1)^2`
`=(-x^2-2x-1+x^2-2x+1-4x^2)/(x^2-1):(4(x+1))/(x-1)`
`=(-4x^2-4x)/((x-1)(x+1)).(x-1)/(4(x+1))`
`=(-4(x-1))/((x-1)(x+1)).(x-1)/(4(x+1))`
`=-4/(x+1).(x-1)/(4(x+1)`
`=(1-x)/(x+1)^2`
`F<-1`
`<=>(1-x-(x+1)^2)/(x+1)^2<0`
Vì `(x+1)^2>0`
`=>1-x-(x+1)^2<0`
`<=>(x+1)^2+x-1>0`
`<=>x^2+2x+1+x-1>0`
`<=>x^2+3x>0`
`<=>x(x+3)>0`
`<=>` $\left[ \begin{array}{l}x>0\\x<-3\end{array} \right.$

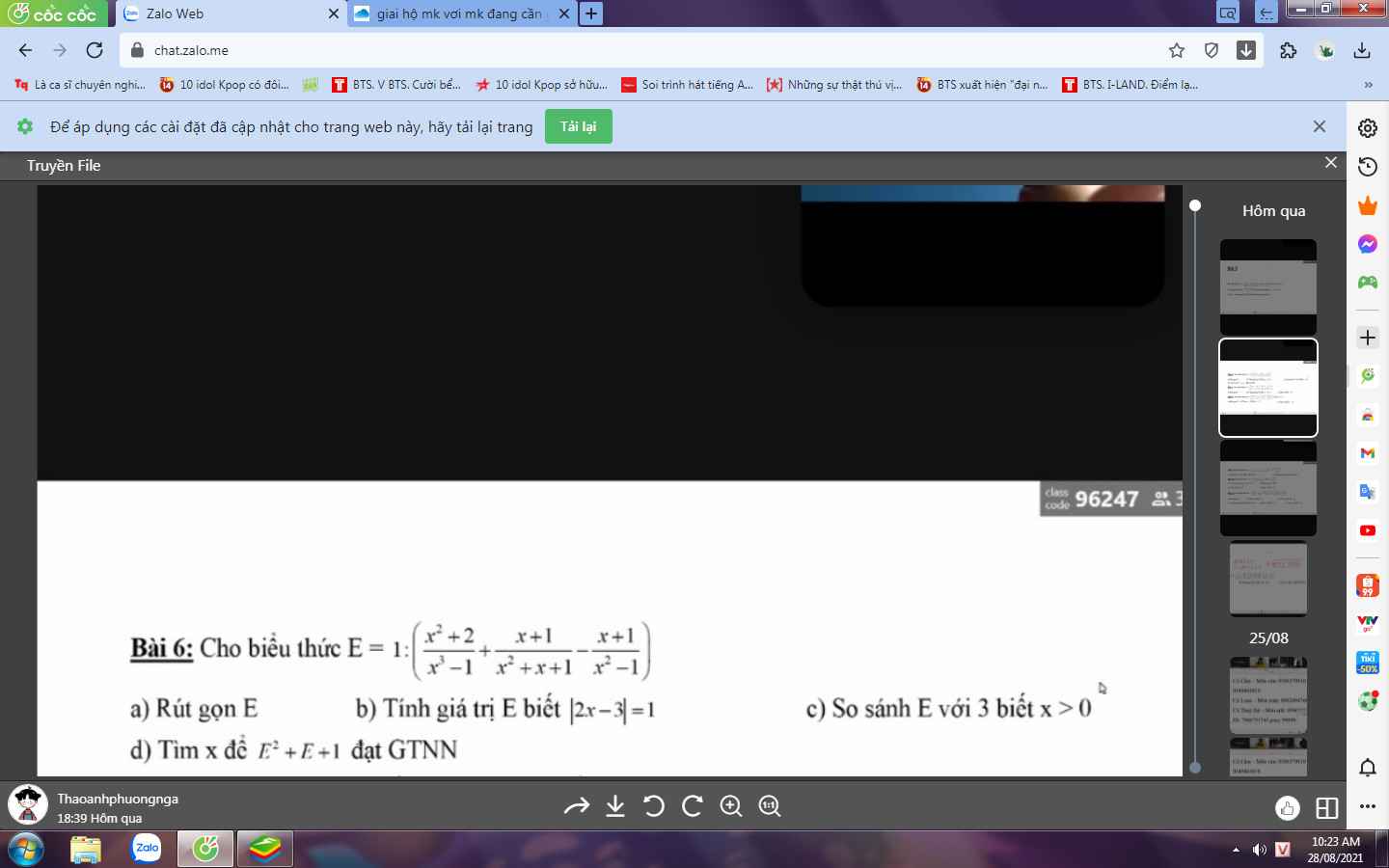
Bài 6:
a: Ta có: \(E=1:\left(\dfrac{x^2+2}{x^3-1}-\dfrac{x+1}{x^2+x+1}-\dfrac{x+1}{x^2-1}\right)\)
\(=1:\left(\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\)
\(=1:\dfrac{x^2+2-x^2+1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-x^2-x+2}\)
\(=\dfrac{-\left(x-1\right)\left(x^2+x+1\right)}{\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-x^2-x-1}{x+2}\)

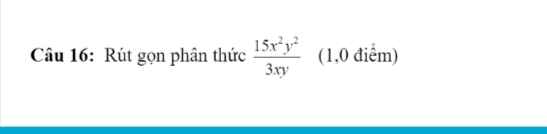

 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá giải giúp mk bài 2 tìm x nhé(trừ câu a,b). Xin cảm ơn trước ạ
giải giúp mk bài 2 tìm x nhé(trừ câu a,b). Xin cảm ơn trước ạ

Bạn ơi ko đc đăng bài thi:)
Mk KT bn ạ chưa thi