K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
Tổng đã cho là tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\dfrac{1}{2}}=2\)
28 tháng 9 2021
\(y=\dfrac{2\left(2cos^2x-1\right)+3sin2x+3}{3-sin2x+cos2x}=\dfrac{3sin2x+2cos2x+3}{3-sin2x+cos2x}\left(\cdot\right)\)
\(\left(\cdot\right)\Leftrightarrow y\left(3-sin2x+cos2x\right)=3sin2x+2cos2x+3\)
\(\Leftrightarrow\left(y+3\right)sin2x+\left(2-y\right)cos2x=3y-3\left(1\right)\)
Để phương trình (1) có nghiệm thì:
\(\left(y+3\right)^2+\left(2-y\right)^2\ge\left(3y-3\right)^2\)
\(\Leftrightarrow7y^2-20y-4\le0\)
\(\Leftrightarrow\dfrac{10-8\sqrt{2}}{7}\le y\le\dfrac{10+8\sqrt{2}}{7}\)
=> min, max của y
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 5 2020
\(y'=-x^2-4x-3=-\left(x+2\right)^2+1\le1\)
Dấu "=" xảy ra khi \(x=-2\)
\(\Rightarrow x_0=-2\) \(\Rightarrow y_0=\frac{5}{3}\)
Phương trình tiếp tuyến:
\(y=1\left(x+2\right)+\frac{5}{3}\Leftrightarrow y=x+\frac{11}{3}\)
25 tháng 4 2023
c: \(\left(x^2+x-3\right)'=2x+1\)
(2x-1)'=2
\(y'=\dfrac{\left(2x+1\right)\cdot\left(2x-1\right)-\left(x^2+x-3\right)\cdot2}{\left(2x-1\right)^2}\)
\(=\dfrac{4x^2-1-2x^2-2x+6}{\left(2x-1\right)^2}=\dfrac{2x^2-2x+5}{\left(2x-1\right)^2}\)
TT
21 tháng 3 2022
1. \(limu_n=-8\)
2. \(lim(-n+6)=\)\(-\infty\)
3. \(lim\left(u_n.v_n\right)=8.\dfrac{7}{2}=4.7=28\)
4. \(lim\dfrac{6n}{n+5}=lim\dfrac{6}{1+\dfrac{5}{n}}=6\)
5. \(lim\left(\dfrac{2}{9}\right)^n=\dfrac{2^n}{9^n}=\dfrac{\left(\dfrac{2}{9}\right)^n}{\left(\dfrac{9}{9}\right)^n}=0\)
TV
giúp mình với ạ Mình cảm ơn
3
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
5.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(\left(1-\dfrac{sinx}{cosx}\right)\left(sin^2x+cos^2x+2sinx.cosx\right)=1+\dfrac{sinx}{cosx}\)
\(\Leftrightarrow\dfrac{\left(cosx-sinx\right)}{cosx}\left(sinx+cosx\right)^2=\dfrac{sinx+cosx}{cosx}\)
\(\Leftrightarrow\dfrac{\left(sinx+cosx\right)\left(cos^2x-sin^2x\right)}{cosx}=\dfrac{sinx+cosx}{cosx}\)
\(\Leftrightarrow\dfrac{cos2x\left(sinx+cosx\right)}{cosx}-\dfrac{sinx+cosx}{cosx}=0\)
\(\Leftrightarrow\dfrac{sinx+cosx}{cosx}\left(cos2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\\cos2x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
6.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos6x-\left(\dfrac{1}{2}+\dfrac{1}{2}cos8x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos10x-\left(\dfrac{1}{2}+\dfrac{1}{2}cos12x\right)\)
\(\Leftrightarrow cos6x-cos10x+cos8x-cos12x=0\)
\(\Leftrightarrow2sin2x.sin8x+2sin2x.sin10x=0\)
\(\Leftrightarrow sin2x\left(sin8x+sin10x\right)=0\)
\(\Leftrightarrow2sin2x.sin9x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sin9x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{k\pi}{9}\end{matrix}\right.\)
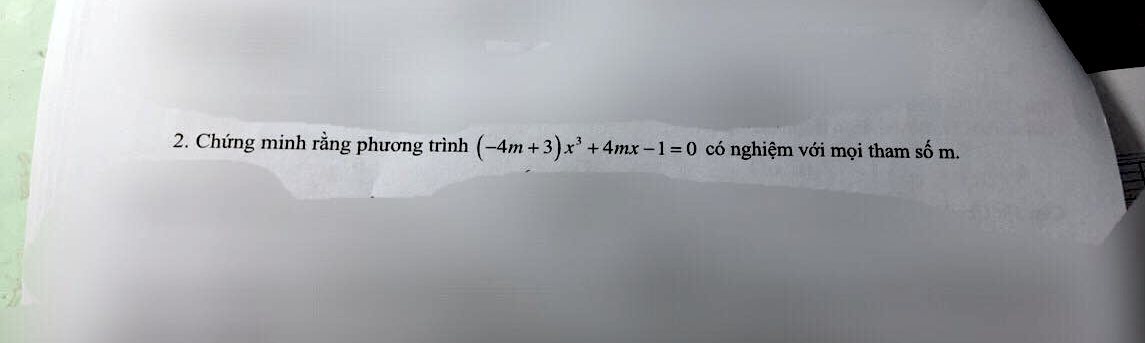
Lời giải:
Xét hàm $f(x)=(-4m+3)x^3+4mx-1$ liên tục trên $R$
$f(1)=-4m+3+4m-1=2>0$
$f(-1)=4m-3-4m-1=-4<0$
$\Rightarrow f(1)f(-1)<0$
Do đó pt $f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(-1;1)$ với mọi $m$ (đpcm)