K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
0
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
Xét phương trình phần đường bao:
\(\left(x+3\right)^2+\left(y+1\right)^2=1\Leftrightarrow\left(y+1\right)^2=1-\left(x+3\right)^2\)
\(\Leftrightarrow y+1=\pm\sqrt{1-\left(x+3\right)^2}\) (với \(-4\le x\le-2\))
\(\Leftrightarrow y=-1\pm\sqrt{1-\left(x+3\right)^2}\)
\(V=\pi\int\limits^{-2}_{-4}\left[\left(-1-\sqrt{1-\left(x+3\right)^2}\right)^2-\left(-1+\sqrt{1-\left(x+3\right)^2}\right)^2\right]dx\)
\(=\pi\int\limits^{-2}_{-4}4\sqrt{1-\left(x+3\right)^2}dx\)
Đặt \(x+3=sint\Rightarrow dx=cost.dt\) ; \(\left\{{}\begin{matrix}x=-4\Rightarrow t=-\dfrac{\pi}{2}\\x=-2\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(V=\pi\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}4cost.cost.dt=2\pi\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\left(1+cos2t\right)=\pi\left(t+\dfrac{1}{2}sin2t\right)|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}=2\pi^2\)
Có vẻ cả 4 đáp án đều không chính xác
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
HK
1
HN
13 tháng 10 2021
Ta có: (u.v)' = u'.v + u.v'
\(Q=80K^{\dfrac{1}{3}}\left(100-K\right)^{\dfrac{1}{2}}\)
\(Q'=80.\left(K^{\dfrac{1}{3}}\right)'.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\left(\left(100-K\right)^{\dfrac{1}{2}}\right)'\)= \(80.\dfrac{1}{3}.K^{-\dfrac{2}{3}}.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\dfrac{1}{2}.\left(100-K\right)^{-\dfrac{1}{2}}.\left(-1\right)\) = \(80.\left(\dfrac{\left(100-K\right)^{\dfrac{1}{2}}}{3K^{\dfrac{2}{3}}}-\dfrac{K^{\dfrac{1}{3}}}{2\left(100-K\right)^{\dfrac{1}{2}}}\right)\)= \(80.\left(\dfrac{2\left(100-K\right)^{\dfrac{1}{2}}\left(100-K\right)^{\dfrac{1}{2}}-3K^{\dfrac{2}{3}}K^{\dfrac{1}{3}}}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{2\left(100-K\right)-3K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{200-5K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(\dfrac{400\left(40-K\right)}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\) = \(\dfrac{200\left(40-K\right)}{3K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\).
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
Lời giải:
Kẻ $SM\perp AB$.
Mà $AB$ là giao tuyến của 2 mp vuông góc với nhau là $(SAB)$ và $(ABCD)$ nên $SM\perp (ABCD)$
$\Rightarrow \angle (SC, (ABCD))=\angle (SC, MC)=\widehat{SCM}$
Ta có:
$\frac{SM^2}{MC^2}=(\tan \widehat{SCM})^2=(\frac{\sqrt{15}}{5})^2=\frac{3}{5}$
$\Rightarrow 5SM^2=3MC^2$
Trong đó:
$SM^2=\frac{3}{4}AB^2$ do $SAB$ là tam giác đều
$MC^2=MB^2+BC^2=\frac{AB^2}{4}+a^2$
$\Rightarrow \frac{15}{4}AB^2=\frac{3}{4}AB^2+3a^2$
$\Rightarrow AB=a$
Vậy:
$SM^2=\frac{3}{4}AB^2=\frac{3}{4}a^2\Rightarrow SM=\frac{\sqrt{3}}{2}a$
$S_{ACD}=\frac{AD.AB}{2}=\frac{2a.a}{2}=a^2$
$V_{S.ABCD}=\frac{1}{3}.SM.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{3}}{2}a.a^2=\frac{\sqrt{3}}{6}a^3$
Đáp án D.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
\(y'=3mx^2-4mx-\left(m+1\right)\)
- Với \(m=0\Rightarrow y'=-1< 0\) hàm nghịch biến trên R (thỏa)
- Với \(m\ne0\) hàm nghịch biến trên R khi:
\(\left\{{}\begin{matrix}3m< 0\\\Delta'=4m^2+3m\left(m+1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\7m^2+3m\le0\\\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{3}{7}\le m< 0\)
Vậy \(-\dfrac{3}{7}\le m\le0\Rightarrow m=0\)
S có 1 phần tử
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
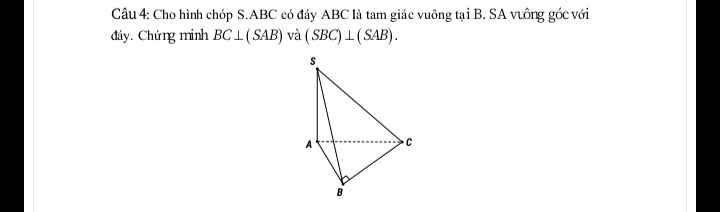
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Lại có \(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAB\right)\)