
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1. a) Công có ích là:
Ai = 10.m.h = 10.900.4 = 36000 (J)
Công toàn phần là:
Atp = Ai/H . 100 = 36000/90 . 100 = 40000 (J)
Công suất của người đó là:
P = Atp/t = 40000 / 1/6 = 240000 (W)
b) Lực nâng vật lên là:
F = Atp/2h = 40000/2.4 = 5000 (N)
c) Công hao phí là:
Ahp = Atp - Ai = 40000 - 36000 = 4000 (J)
(KHẨN CẤP: phần lực ma sát mình chỉ chắc cách 1 thôi nhé, cách 2 là ý kiến riêng của mình)
C1: Lực ma sát là:
Fms = Ahp/2h = 4000/2.4 = 500 (N)
C2: Lực ma sát là:
Fms = (Atp.10%)/2h = (40000.10%)/2.4 = 500 (N)
2. a) 10m/phút = 1/6m / giây
Công suất của lực kéo trên là:
P = A/t = F.S / t = 4500.1/6 / 1 = 750 (W)
b) 15m/phút = 0,25m/ giây
Công suất của lực kéo trên là:
P = A/t = F.S / t = 4500.0,25 / 1 = 1125 (W)
3. a) Công có ích là:
Ai = 10.m.h = 10.50.8 = 4000 (J)
b) Công toàn phần là:
Atp = Ai/H . 100 = 4000/80 . 100 = 5000 (J)
c) Lực kéo vật lên là:
F = Atp/2h = 5000/2.8 = 312,5 (N)
d) Công hao phí là:
Ahp = Atp - Ai = 5000-4000 = 1000 (J)
Lực ma sát là:
Fms = Ahp/2h = 1000/2.8 = 62,5 (N)
Chúc bạn thi tốt!

mình cho đáp án luôn
- . ĐỀ 1 ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN MÔN: TOÁN LỚP 8 Thời gian: 150 phút Bài 1: (3đ) a) Phân tích đa thức x3 – 5x2 + 8x – 4 thành nhân tử b) Tìm giá trị nguyên của x để A M B biết A = 10x2 – 7x – 5 và B = 2x – 3 . c) Cho x + y = 1 và x y ≠ 0 . Chứng minh rằng ( ) 3 3 2 2 2 0 1 1 3 x yx y y x x y − − + = − − + Bài 2: (3đ) Giải các phương trình sau: a) (x2 + x)2 + 4(x2 + x) = 12 b) 2003 6 2004 5 2005 4 2006 3 2007 2 2008 1 + + + + + = + + + + + xxxxxx Bài 3: (2đ) Cho hình vuông ABCD; Trên tia đối tia BA lấy E, trên tia đối tia CB lấy F sao cho AE = CF a) Chứng minh ∆EDF vuông cân b) Gọi O là giao điểm của 2 đường chéo AC và BD. Gọi I là trung điểm EF. Chứng minh O, C, I thẳng hàng. Bài 4: (2)Cho tam giác ABC vuông cân tại A. Các điểm D, E theo thứ tự di chuyển trên AB, AC sao cho BD = AE. Xác địnhvị trí điểm D, E sao cho: a/ DE có độ dài nhỏ nhất b/ Tứ giác BDEC có diện tích nhỏ nhất.
- 2. HD CHẤM Bài 1: (3 điểm) a) ( 0,75đ) x3 - 5x2 + 8x - 4 = x3 - 4x2 + 4x – x2 + 4x – 4 (0,25đ) = x( x2 – 4x + 4) – ( x2 – 4x + 4) (0,25đ) = ( x – 1 ) ( x – 2 ) 2 (0,25đ) b) (0,75đ) Xét 2 A 10x 7x 5 7 5x 4 B 2x 3 2x 3 − − = = + + − − (0,25đ) Với x ∈ Z thì A M B khi 7 2 3−x ∈ Z ⇒ 7 M ( 2x – 3) (0,25đ) Mà Ư(7) = { }1;1; 7;7− − ⇒ x = 5; - 2; 2 ; 1 thì A M B (0,25đ) c) (1,5đ) Biến đổi 3 3 x y y 1 x 1 − − − = 4 4 3 3 x x y y (y 1)(x 1) − − + − − = ( )4 4 2 2 x y (x y) xy(y y 1)(x x 1) − − − + + + + ( do x + y = 1⇒ y - 1= -x và x - 1= - y) (0,25đ) = ( ) ( ) ( )2 2 2 2 2 2 2 2 x y x y x y (x y) xy(x y y x y yx xy y x x 1) − + + − − + + + + + + + + (0,25đ) = ( ) 2 2 2 2 2 2 x y (x y 1) xy x y xy(x y) x y xy 2 − + − + + + + + + (0,25đ) = ( ) 2 2 2 2 2 x y (x x y y) xy x y (x y) 2 − − + − + + + = ( )[ ] 2 2 x y x(x 1) y(y 1) xy(x y 3) − − + − + (0,25đ) = ( )[ ] 2 2 x y x( y) y( x) xy(x y 3) − − + − + = ( ) 2 2 x y ( 2xy) xy(x y 3) − − + (0,25đ) = 2 2 2(x y) x y 3 − − + Suy ra điều cần chứng minh (0,25đ) Bài 2: (3 đ)a) (1,25đ) (x2 + x )2 + 4(x2 + x) = 12 đặt y = x2 + x y2 + 4y - 12 = 0 ⇔ y2 + 6y - 2y -12 = 0 (0,25đ) ⇔ (y + 6)(y - 2) = 0 ⇔ y = - 6; y = 2 (0,25đ) * x2 + x = - 6 vô nghiệm vì x2 + x + 6 > 0 với mọi x (0,25đ) * x2 + x = 2 ⇔ x2 + x - 2 = 0 ⇔ x2 + 2x - x - 2 = 0 (0,25đ) ⇔ x(x + 2) – (x + 2) = 0 ⇔ (x + 2)(x - 1) = 0 ⇔ x = - 2; x = 1 (0,25đ) Vậy nghiệm của phương trình x = - 2 ; x =1 b) (1,75đ) x 1 x 2 x 3 x 4 x 5 x 6 2008 2007 2006 2005 2004 2003 + + + + + + + + = + + ⇔ x 1 x 2 x 3 x 4 x 5 x 6 ( 1) ( 1) ( 1) ( 1) ( 1) ( 1) 2008 2007 2006 2005 2004 2003 + + + + + + + + + + + = + + + + +
- 3. ⇔ 2003 2009 2004 2009 2005 2009 2006 2009 2007 2009 2008 2009 + + + + + = + + + + + xxxxxx ⇔ x 2009 x 2009 x 2009 x 2009 x 2009 x 2009 0 2008 2007 2006 2005 2004 2003 + + + + + + + + − − − = (0,25đ) ⇔ 0) 2003 1 2004 1 2005 1 2006 1 2007 1 2008 1 )(2009( =−−−+++x (0,5đ) Vì 1 1 2008 2005 < ; 1 1 2007 2004 < ; 1 1 2006 2003 < Do đó : 0 2003 1 2004 1 2005 1 2006 1 2007 1 2008 1 <−−−++ (0,25đ) Vậy x + 2009 = 0 ⇔ x = -2009 Bài 3: (2 điểm) a) (1đ) Chứng minh ∆EDF vuông cân Ta có ∆ADE = ∆CDF (c.g.c)⇒ ∆EDF cân tại D Mặt khác: ∆ADE = ∆CDF (c.g.c) ⇒ 1 2 ˆ ˆE F= Mà 1 2 1 ˆ ˆ ˆE E F+ + = 900 ⇒ 2 2 1 ˆ ˆ ˆF E F+ + = 900 ⇒ EDF= 900 . Vậy ∆EDF vuông cân b) (1đ) Chứng minh O, C, I thẳng Theo tính chất đường chéo hình vuông ⇒ CO là trung trực BD Mà ∆EDF vuông cân ⇒ DI = 1 2 EF Tương tự BI = 1 2 EF ⇒ DI = BI ⇒ I thuộc dường trung trực của DB ⇒ I thuộc đường thẳng CO Hay O, C, I thẳng hàng Bài 4: (2 điểm) a) (1đ) DE có độ dài nhỏ nhất Đặt AB = AC = a không đổi; AE = BD = x (0 < x < a) Áp dụng định lý Pitago với ∆ADE vuông tại A có: DE2 = AD2 + AE2 = (a – x)2 + x2 = 2x2 – 2ax + a2 = 2(x2 – ax) – a2 (0,25đ) = 2(x – 2 a 4 )2 + 2 a 2 ≥ 2 a 2 (0,25đ) Ta có DE nhỏ nhất ⇔ DE2 nhỏ nhất ⇔ x = a 2 (0,25đ) A B E I D C O F 2 1 1 2 A D B C E
- 4. ⇔ BD = AE = a 2 ⇔ D, E là trung điểm AB, AC (0,25đ) b) (1đ) Tứ giác BDEC có diện tích nhỏ nhất. Ta có: SADE = 1 2 AD.AE = 1 2 AD.BD = 1 2 AD(AB – AD)= 1 2 (AD2 – AB.AD) (0,25đ) = – 1 2 (AD2 – 2 AB 2 .AD + 2 AB 4 ) + 2 AB 8 = – 1 2 (AD – AB 4 )2 + 2 AB 2 ≤ 2 AB 8 (0,25đ) Vậy SBDEC = SABC – SADE ≥ 2 AB 2 – 2 AB 8 = 3 8 AB2 không đổi (0,25đ) Do đó min SBDEC = 3 8 AB2 khi D, E lần lượt là trung điểm AB, AC (0,25đ)

Công suất ng đó là
\(P=\dfrac{A}{t}=\dfrac{P.h}{t}=\dfrac{10m.h}{t}\\ =\dfrac{10.30.4}{50}=24W\)

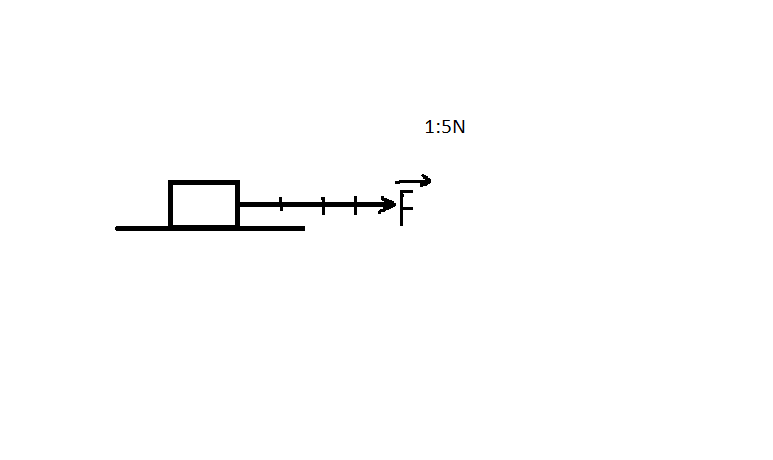
Phương ngang.
Chiều từ trái sang phải.
Độ lớn: \(F=20N\)
 Giúp mình với mấy bạn,sắp thi rồi
Giúp mình với mấy bạn,sắp thi rồi Các bạn giúp mình làm câu 1, 2.b, 3,4 vs
Các bạn giúp mình làm câu 1, 2.b, 3,4 vs 





 ai giúp mình làm đống này với chỉ cần trả lời câu mấy ý mấy là được rồi ạ
ai giúp mình làm đống này với chỉ cần trả lời câu mấy ý mấy là được rồi ạ
oke pn :V
Bài 23 : Giải :
Vì hai bình nước giống nhau, cùng chứa 1 lượng nước như nhau.
\(\Rightarrow m_1=m_2;c_1=c_2\)
Vì \(t_2=2t_1\) => Bình 2 tỏa nhiệt, bình 1 thu nhiệt.
Nhiệt lượng tỏa ra của bình 2 là :
\(Q_{tỏa}=m_2c_2\left(t_2-t\right)\)
Nhiệt lượng thu vào của bình 1 là :
\(Q_{thu}=m_1c_1\left(t-t_1\right)\)
Theo ptcb nhiệt : \(Q_{tỏa}=Q_{thu}\)
\(\Leftrightarrow m_2c_2\left(t_2-t\right)=m_1c_1\left(t-t_1\right)\)
Đơn giản biểu thức :
\(\Leftrightarrow2t_1-36=36-t_1\)
\(\Rightarrow t_1=24^oC\)
Vậy nhiệt độ \(t_2=2\cdot24=48^oC\)
NĐộ ban đầu của bình 1 là 24 độ C, bình 2 là 48 độ C.
Bài 24 :
Tóm tắt :
\(m_1=600g=0,6kg\)
\(t_1=100^oC\)
\(m_2=2,5kg\)
\(t=30^oC\)
\(c_1=380Jkg.K\)
\(c_2=4200Jkg.K\)
\(t-t_2=?\)
Giải :
Nhiệt lượng tỏa ra của quả cầu đồng là :
\(Q_{tỏa}=m_1c_1\left(t_1-t\right)\)
Nhiệt lượng thu vào của nước là :
\(Q_{thu}=m_2c_2\left(t-t_2\right)\)
Theo PTCB nhiệt :
\(Q_{tỏa}=Q_{thu}\)
\(\Leftrightarrow m_1c_1\left(t_1-t\right)=m_2c_2\left(t-t_2\right)\)
\(\Leftrightarrow0,6\cdot380\cdot\left(100-30\right)=2,5\cdot4200\cdot\left(30-t_2\right)\)
\(\Rightarrow t_2=28,48^oC\)
Vậy nước nóng thêm : \(30-28,48=1,52^oC\)