K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2
19 tháng 5 2023
`10)`
Xếp `6` học sinh vào `7` chỗ là `2` lần hoán vị của `6`
`=>` Có `2.6!=1440` cách.
`11)` Chọn `3` học sinh trong `8` học sinh là chỉnh hợp chập `3` của `8`
`=>` Có `A_8 ^3=336` cách.
LD
19 tháng 5 2023
Xếp 6 học sinh vào 7 chỗ là 2 lần hoán vị của 6
⇒ Có 2.6≠1440 cách.
11) Chọn 33 học sinh trong 88 học sinh là chỉnh hợp chập 33 của 88
⇒ Có \(a\dfrac{3}{8}\)=336 cách.
2
19 tháng 5 2023
`\Omega=C_38 ^3`
Gọi `A:`"Chọn `3` học sinh là nam."
`=>A=C_18 ^3`
`=>P(A)=[C_18 ^3]/[C_38 ^3]=68/703`
LD
19 tháng 5 2023
\(\Omega=c\dfrac{3}{28}\)
gọi a là chọn 3 học sinh là nam
a=\(c\dfrac{3}{18}\)
p(a)=\(\dfrac{c\dfrac{3}{18}}{c\dfrac{3}{38}}\)=\(\dfrac{68}{703}\)
16 tháng 5 2023
4:
\(n\left(\Omega\right)=C^3_{35}\)
\(n\left(A\right)=C^3_{15}\)
=>\(P\left(A\right)=\dfrac{13}{187}\)
LD
19 tháng 5 2023
\(\left\{{}\begin{matrix}x=1+t\\y=2+2t\end{matrix}\right.\)
--->vtcp là \(\overrightarrow{u}\)=(1;2)
Y
19 tháng 5 2023
\(n\left(\Omega\right)=2^3=8\)
Gọi A : '' Nhận 2 mặt sấp ''
\(A=\left\{SNS;SSN;NSS;SSS\right\}\Rightarrow n\left(A\right)=4\)
Xác suất biến cố \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{8}=\dfrac{1}{2}\)
2
19 tháng 5 2023
Ptr tổng quát đi qua `A(4;2)` và có `\vec{n}=(-1;2)` là:
`-(x-4)+2(y-2)=0`
`<=>-x+2y=0`
LD
19 tháng 5 2023
Ptr tổng quát đi qua A(4;2) và có\(\overrightarrow{n}\)=(-1;2)
-(x-4) +2(y-2)=0
⇔ - x+2y=0
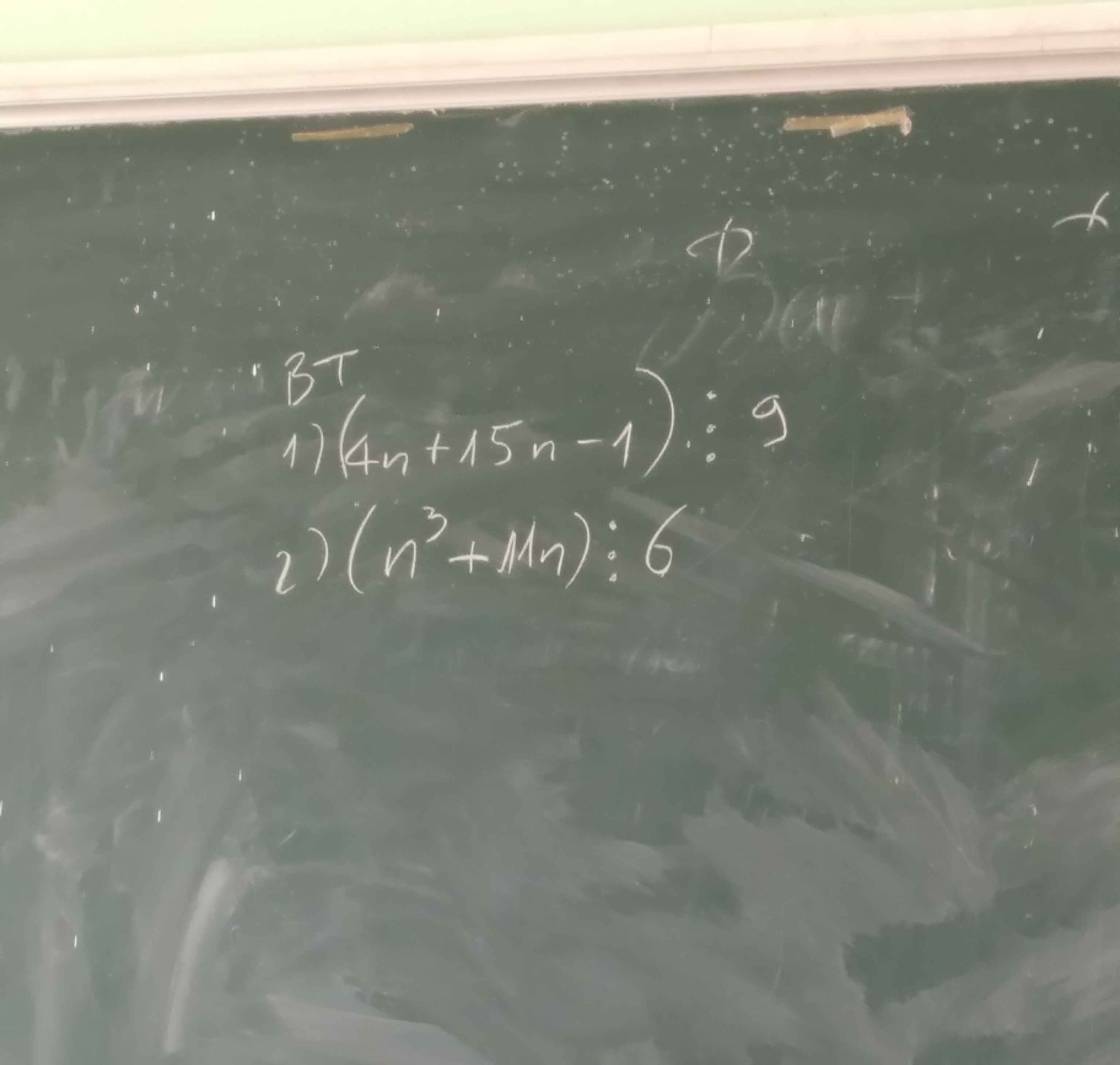
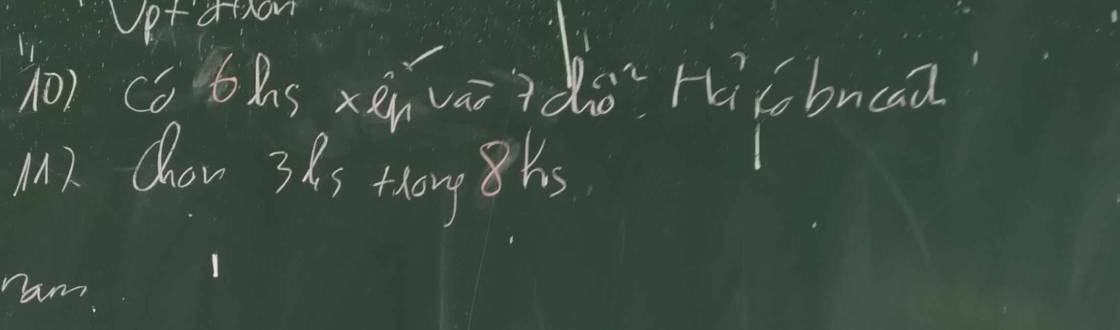
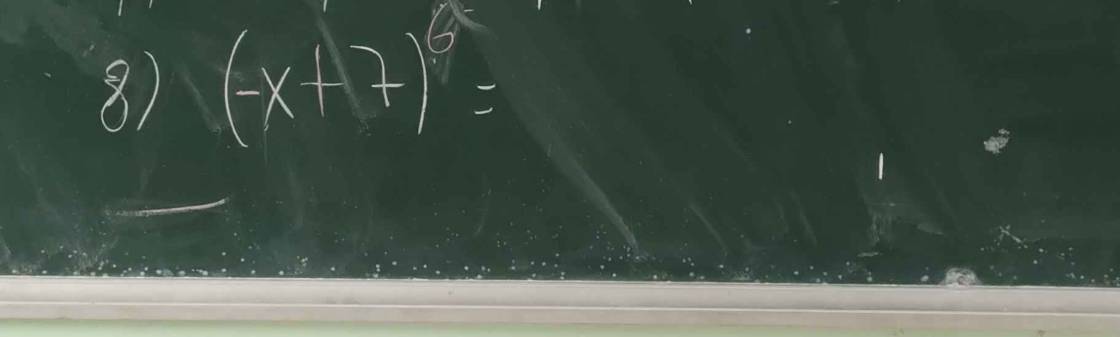
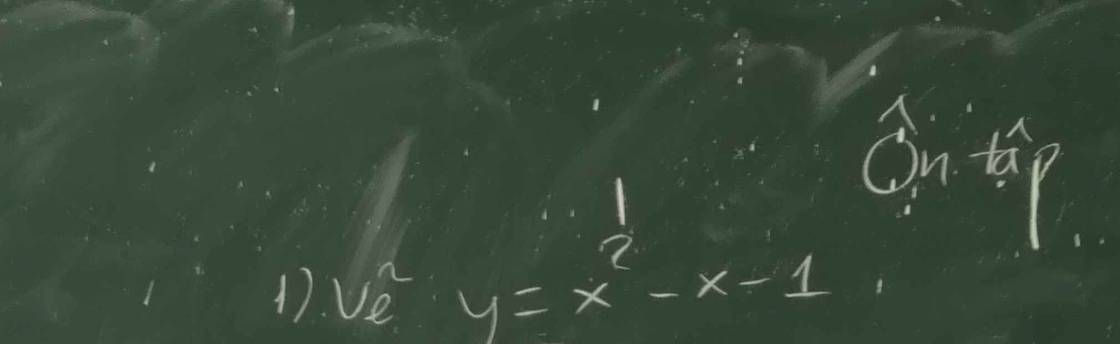
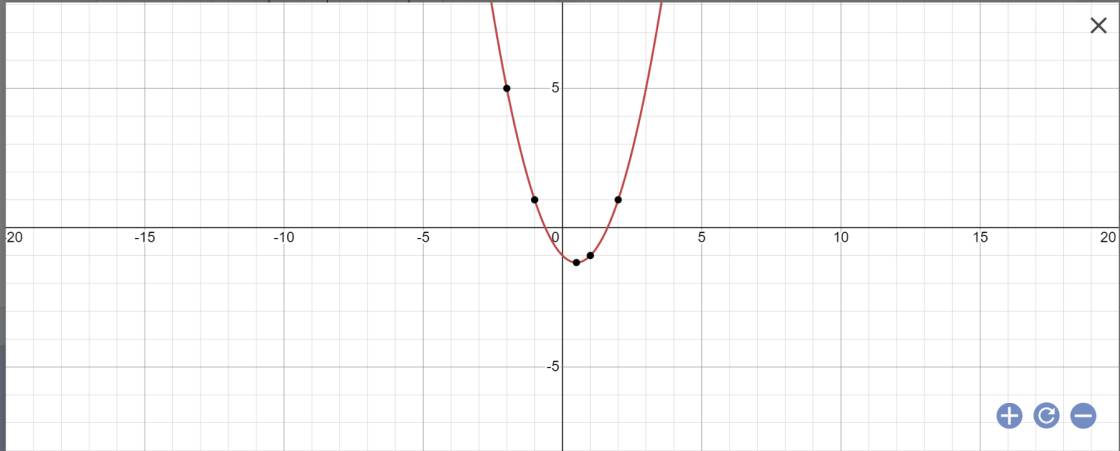
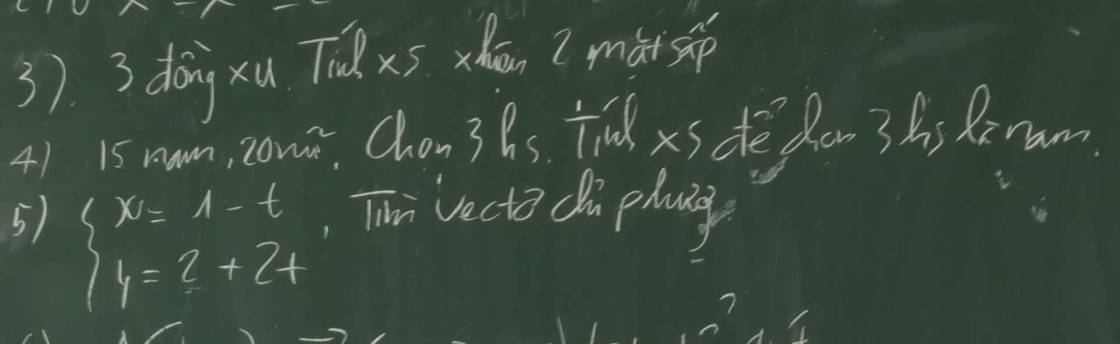
Câu a xem lại đề em nhé
b) Ta có:
\(n^3+11n=n^3+n-12n\)
\(=n\left(n^2-1\right)+12n\)
\(=n\left(n-1\right)\left(n+1\right)+12n\)
Do \(n\left(n-1\right)\) là tích của hai số nguyên liên tiếp nên chia hết cho 2
Do \(n\left(n-1\right)\left(n+1\right)\) là tích của ba số nguyên liên tiếp nên chia hết cho 3
\(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮6\)
Lại có \(12n⋮6\)
\(\Rightarrow\left[n\left(n-1\right)\left(n+1\right)+12n\right]⋮6\)
Vậy \(\left(n^3-11n\right)⋮6\)
Sửa đề câu a
\(\left(4^n+15n-1\right)⋮9\)
Giải
Đặt \(A_n=4^n+15n-1\)
- Với n = 1 \(\Rightarrow A_1=4+15-1=18⋮9\)
- Giả sử đúng với \(n=k\ge1\) nghĩa là:
\(A_k=\left(4^k+15k-1\right)⋮9\) (giả thiết quy nạp)
Ta cần chứng minh: \(A_{k+1}⋮9\)
Thật vậy, ta có:
\(A_{k+1}=4^{k+1}+15\left(k+1\right)-1\)
\(=4.4^k+15k+15-1\)
\(=4\left(4^k+15k-1\right)-45k+4+15-1\)
\(=4\left(4^k+15k-1\right)-45k+18\)
\(=4A_k-45k+18\)
Do \(A_k⋮9\)
\(-45k+18=-9\left(5k-2\right)⋮9\)
\(\Rightarrow A_{k+1}=\left(4A_k-45k+18\right)⋮9\)
Vậy \(\left(4^n+15n-1\right)⋮9\) \(\forall n\in N\)*