Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>D nằm trên đường trung trực của BM(1)
Ta có: AB=AM
=>A nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
=>AD\(\perp\)BM tại I và I là trung điểm của BM
c: Xét ΔKBA và ΔKPM có
KB=KP
\(\widehat{BKA}=\widehat{PKM}\)(hai góc đối đỉnh)
KA=KM
Do đó: ΔKBA=ΔKPM
=>\(\widehat{KBA}=\widehat{KPM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MP
b) Vì AC=2AB
AB=BD
=>AC=AD
Xét tam giác ACE và tam giác ADE có:
AC=AD ( chứng minh trên )
^CAE=^EAD ( tính chất phân giác )
AE chung
=> tam giác ACE = tam giác ADE ( c.g.c )
=> ^CEA=^AED ( 2 góc tương ứng )
Mà ^CEA kề bù ^AED
=> ^CEA=^AED=90°
=> AE vuông góc CD
AI và AE là 2 tia trùng nhau
=> AI vuông góc CD
Vì AI vuông góc BM
Mà AI vuông góc CD
<=> BM // CD
Chúc bạn học tốt!
Vì mình không tìm được cách gõ góc nên kí hiệu ^ là góc nhé! Mong bạn thông cảm
a) Xét ΔABH,ΔAKHΔABH,ΔAKH có:
BH=HK(gt)BH=HK(gt)
ˆAHB=ˆAHKAHB^=AHK^
AH: cạnh chung
⇒ΔABH=ΔAKH(c−g−c)⇒ΔABH=ΔAKH(c−g−c)
b) Vì ΔABH=ΔAKHΔABH=ΔAKH
⇒AB=AK⇒AB=AK ( cạnh tương ứng ) (1)
Xét ΔAMK,ΔCMEΔAMK,ΔCME có:
AM=MC(=12AC)AM=MC(=12AC)
ˆM1=ˆM2M1^=M2^ ( đối đỉnh )
EM=KM(gt)EM=KM(gt)
⇒ΔAMK=ΔCME(c−g−c)⇒ΔAMK=ΔCME(c−g−c)
⇒EC=AK⇒EC=AK ( cạnh tương ứng ) (2)
Từ (1) và (2) ⇒EC=AB(=AK)⇒EC=AB(=AK)
c) Xét ΔAMEΔAME và ΔCMKΔCMK có:
AM=MC(=12AC)AM=MC(=12AC)
ˆM3=ˆM4M3^=M4^ ( đối đỉnh )
KM=EM(gt)KM=EM(gt)
⇒ΔAME=ΔCMK(c−g−c)⇒ΔAME=ΔCMK(c−g−c)
⇒ˆE1=ˆK1⇒E1^=K1^ ( góc tương ứng )
Mà ˆE1E1^ và ˆK1K1^ ở vị trí so le trong nên AE // KC hay AE // BC
Vậy a) ΔABH=ΔAKH
| GT | △ABC cân tại A. BM ⊥ AC, CN ⊥ AB. BM ∩ CN = {K}. AK ∩ BC = {H}. MD = MK ; NE = NK |
KL | a. BM = CN b, AK là p/g BAC c, AK ⊥ BC d, △AED cân |
Bài giải:
a, Xét △BMA vuông tại M và △CNA vuông tại N
Có: AB = AC (△ABC cân tại A)
BAC là góc chung
=> △BMA = △CNA (ch-gn)
=> BM = CN (2 cạnh tương ứng)
b, Xét △NKA vuông tại N và △MKA vuông tại M
Có: AN = AM (△BMA = △CNA)
AK là cạnh chung
=> △NKA = △MKA (ch-cgv)
=> NAK = MAK (2 góc tương ứng) (1)
Và AK nằm giữa AN và AM
Mà N 
=> AK nằm giữa AB và AC (2)
Từ (1) và (2)
=> AK là phân giác BAC
c, Xét △BAH và △CAH
Có: BA = CA (cmt)
BAH = CAH (cmt)
AH là cạnh chung
=> △BAH = △CAH (c.g.c)
=> BHA = CHA (2 góc tương ứng)
Mà BHA + CHA = 180o (2 góc kề bù)
=> BHA = CHA = 180o : 2 = 90o
=> AH ⊥ BC
Mà AK ∩ BC = {H}
=> AK ⊥ BC
d, Xét △NEA vuông tại N và △NKA vuông tại N
Có: NE = NK (gt)
AN là cạnh chung
=> △NEA = △NKA (2cgv)
=> AE = AK (2 cạnh tương ứng)
Xét △DMA vuông tại M và △KMA vuông tại M
Có: MD = MK (gt)
AM là cạnh chung
=> △DMA = △KMA (2cgv)
=> AD = AK (2 cạnh tương ứng)
Mà AE = AK (cmt)
=> AD = AE
Xét △ADE có: AD = AE (cmt) => △ADE cân tại A
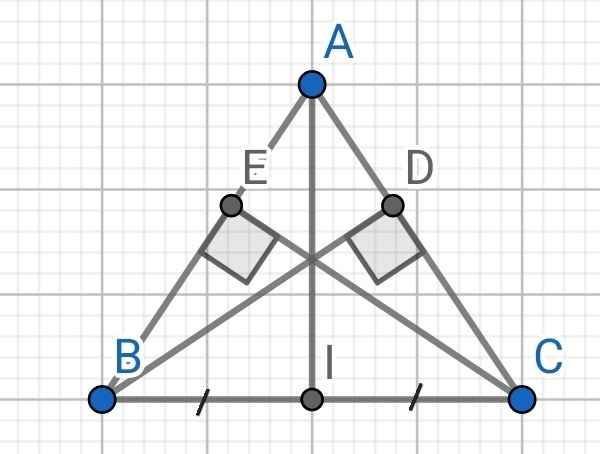a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC