Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
d)
Xét ΔABC cân tại A, ta có:
CD là đường trung tuyến(D là trung điểm AB)
=> CD⊥AB
Xét ΔABC vuông tại D, ta có:
AC2=AD2+CD2(đ/l Py-ta-go)(1)
Ta có: \(\begin{cases} AD+BD=AB(D là trung điểm AB)\\ AE+CE=AC(E là trung điểm AC) \end{cases}\)
Mà : AB=AC(ΔABC cân tại A)
Nên: AD=AE
=>ΔADE cân tại A
Mà DM là trung tuyến ( M là trung điểm AE)
Suy ra: DM⊥AE
Xét △AMD vuông tại M ta có:
AD2 = AM2+ MD2 (định lý Py-ta-go) (2)
Xét △DMC vuông tại M ta có:
CD2 = MC2 +MD2 (định lý Py-ta-go) (3)
Từ (2) và (3) suy ra:
AD2+ CD2 = AM2+MD2+MC2+MD2
= AM2+2MD2+MC2
Thay vào (1) ta có:
AC2= MA2+2MD2+MC2
=> 2MD2= AC2-MA2-MC2
=> 2MD2=(MA+MC)2-MA2-MC2
=> 2MD2=MA2+2MA.MC+MC2-MA2-MC2
=> 2MD2=2.MA.MC
=> MD2=MA.MC (đpcm)
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//BC và DE=BC/2
hay DE//BF và DE=BF
=>BDEF là hình bình hành
b: Xét tứ giác AMCF có
E là trung điểm của AC
E là trung điểm của MF
Do đó: AMCF là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCF là hình chữ nhật
Để chứng minh các phần a, b và c, ta sẽ sử dụng các tính chất của tam giác vuông và hình chữ nhật.
a. Ta có tam giác ABC vuông tại A, nên theo định lí trung tuyến, ta có DE là đường trung tuyến của tam giác ABC. Do đó, DE song song với cạnh AC. Tương tự, ta có DF song song với cạnh AB. Vậy DE//AC và DF//AB.
b. Ta cần chứng minh AEDF là hình chữ nhật. Đầu tiên, ta thấy DE//AC và DF//AB (theo phần a). Khi đó, ta có:
- AD = DC (vì D là trung điểm của BC)
- AE = EB (vì E là trung điểm của AB)
- AF = FC (vì F là trung điểm của AC)
Vậy ta có các cạnh đối diện của tứ giác AEDF bằng nhau, do đó AEDF là hình chữ nhật.
c. Gọi M là điểm đối xứng của D qua AB. Ta cần chứng minh M đối xứng với N qua A. Để làm điều này, ta sẽ chứng minh AM = AN và góc MAN = góc NAM.
- Vì M là điểm đối xứng của D qua AB, nên ta có AM = AD.
- Vì N là điểm đối xứng của D qua AC, nên ta có AN = AD.
Do đó, ta có AM = AN.
- Ta có góc MAD = góc DAB (vì M là điểm đối xứng của D qua AB)
- Ta có góc NAD = góc DAC (vì N là điểm đối xứng của D qua AC)
Vì tam giác ABC vuông tại A, nên góc DAB = góc DAC. Từ đó, ta có góc MAD = góc NAD.
Vậy ta có AM = AN và góc MAN = góc NAM, do đó M đối xứng với N qua A.
Vậy ta đã chứng minh được M đối xứng với N qua A.
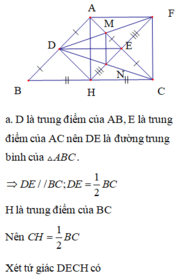
c) Từ kết quả câu a, b có M là trung điểm DF, N là trung điểm DC => MN là đường trung bình của tam giác FDC => MN // FC// AH
AH vuong góc với BC, BC//DE nên MN vuong góc với DE