K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp mình câu 22 với
18 tháng 8 2023
22:
a:
\(\overrightarrow{AD}=2\overrightarrow{DB}\)
=>\(\overrightarrow{AD}=\dfrac{2}{3}\overrightarrow{AB}\)
\(\overrightarrow{CE}=3\overrightarrow{EA}\)
=>\(\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{EC}\)
=>\(\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AC}\)
Xét ΔAED có AM là trung tuyến
nên \(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}\)
b: \(\overrightarrow{MI}=\overrightarrow{ME}+\overrightarrow{EI}\)
\(=\dfrac{1}{2}\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CI}\)
\(=\dfrac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AE}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{-1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Câu 22:
TXĐ: $(-\infty;0]\cup [2;+\infty)$
BPT \(\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x^2-2x\leq (x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x\geq \frac{-1}{4}\end{matrix}\right.\Leftrightarrow x\geq \frac{-1}{4}\)
Kết hợp ĐKXĐ suy ra BPT có nghiệm $[\frac{-1}{4};0]\cup [2;+\infty)$
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Câu 23:
Theo công thức trung tuyến:
$CM^2=\frac{BC^2+AC^2}{2}-\frac{AB^2}{4}=\frac{23}{2}$
Áp dụng công thức Herong cho tam giác $ABC$:
$S_{ABC}=\sqrt{\frac{9}{2}(\frac{9}{2}-2)(\frac{9}{2}-3)(\frac{9}{2}-4)}=\frac{3\sqrt{15}}{4}$
$S_{BCM}=\frac{1}{2}S_{ABC}=\frac{3\sqrt{15}}{8}$
Áp dụng công thức: $S=\frac{abc}{4R}$ cho tam giác $BCM$ thì bán kính đường tròn ngoại tiếp tam giác là:
$R=\frac{BC.CM.BM}{4S_{BCM}}=\frac{4.\sqrt{\frac{23}{2}}.1}{\frac{3\sqrt{15}}{2}}=\frac{4\sqrt{690}}{45}$
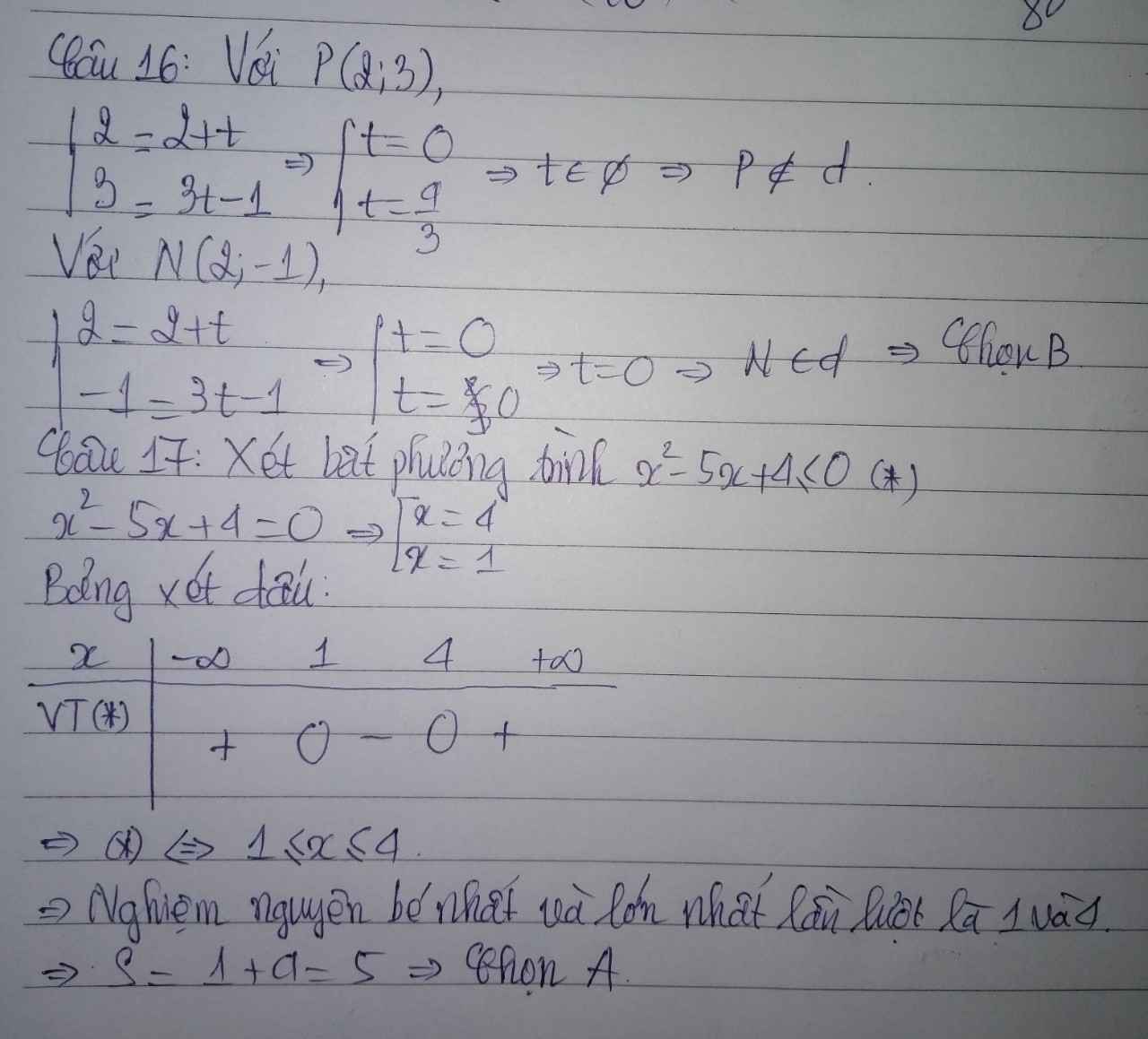
giúp mình mấy câu này với mình cảm ơn nhìu ạ
\(P=\left(sin^2x-1\right)tan^2x+\left(cos^2x-1\right)cot^2x\)
\(=-cos^2x.\dfrac{sin^2x}{cos^2x}+\left(-sin^2x\right)\dfrac{cos^2x}{sin^2x}\)
\(=-sin^2x-cos^2x\)
\(=-\left(sin^2x+cos^2x\right)\)
\(=-1\)