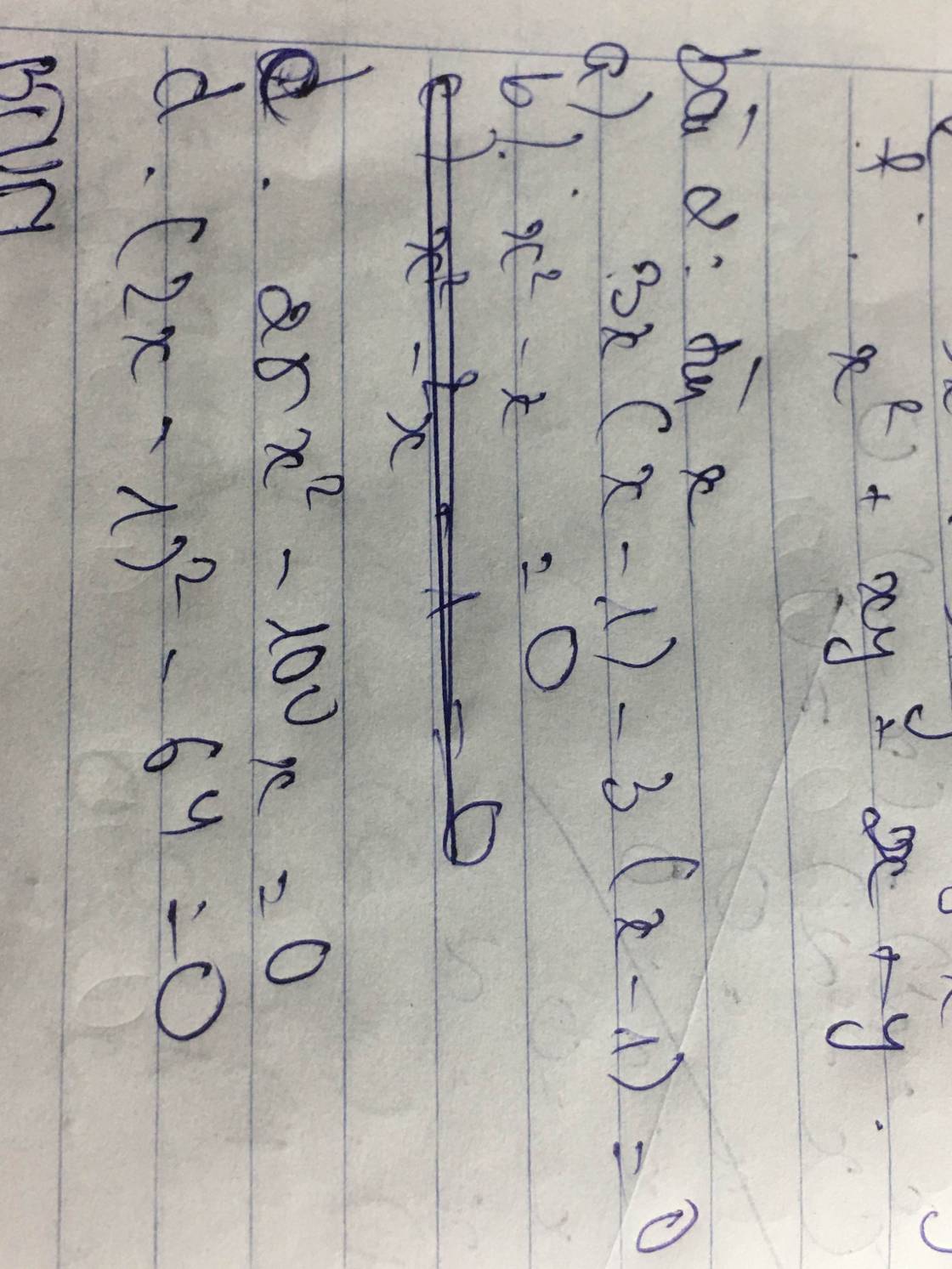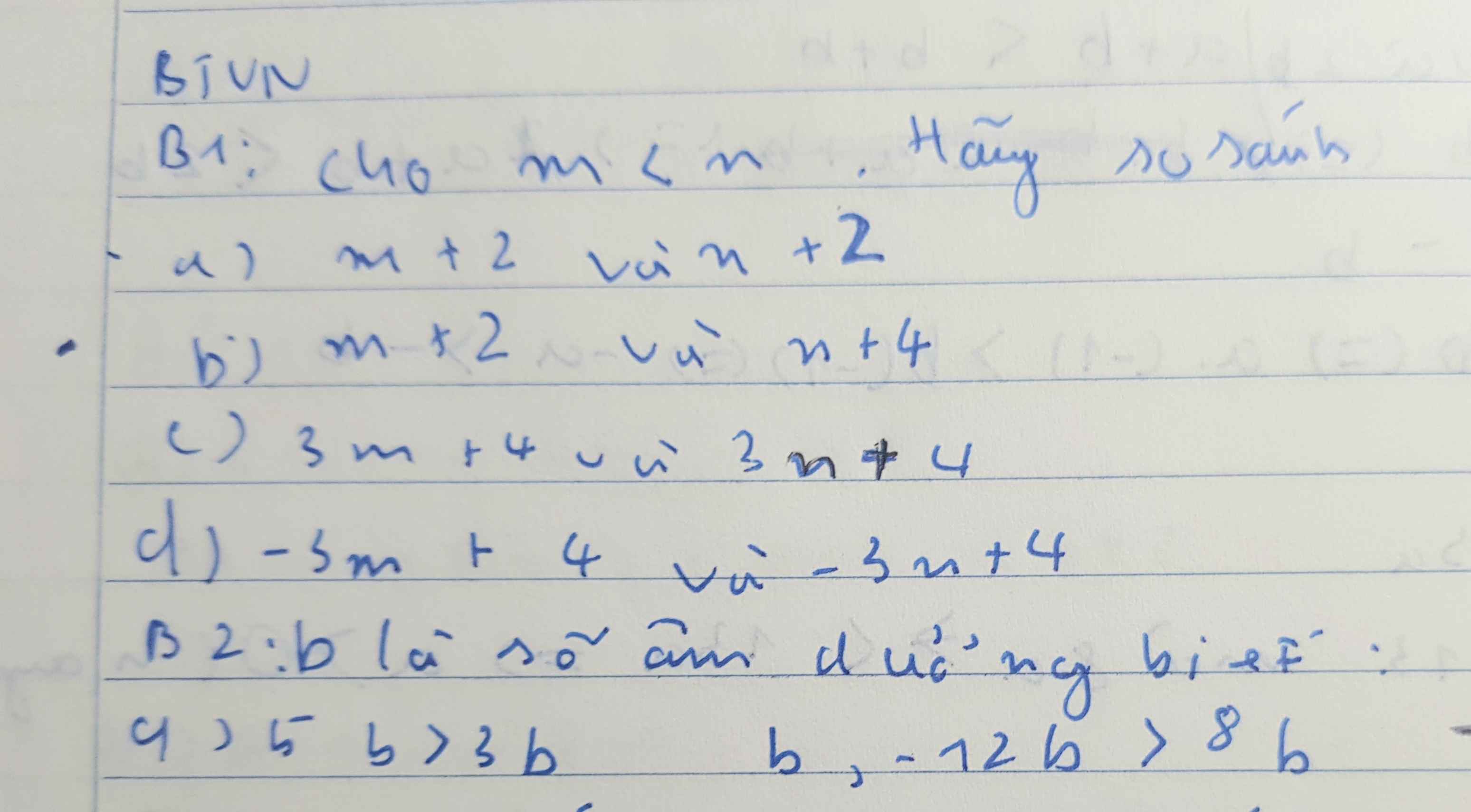K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
1
22 tháng 9 2021
Bài 1:
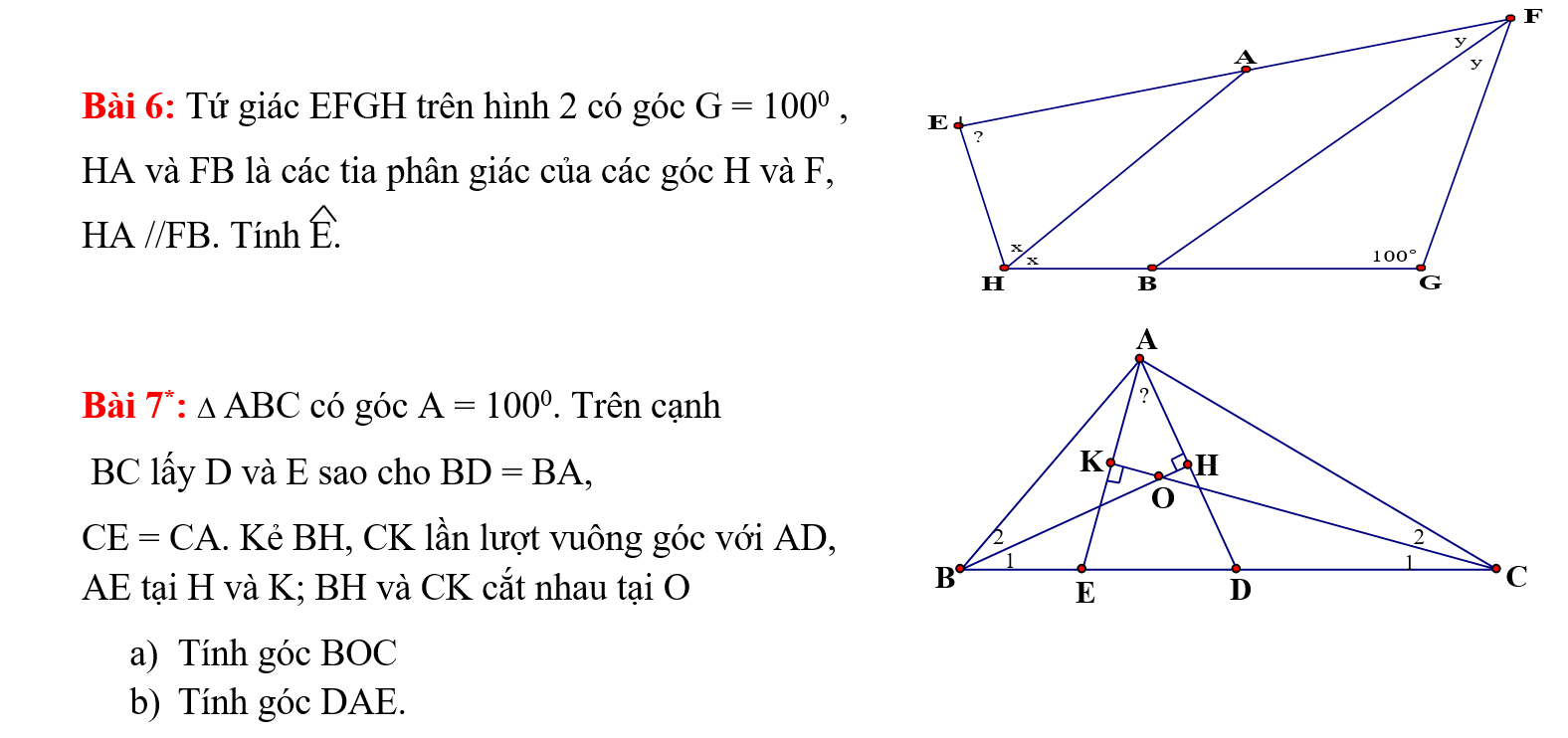
a: Xét tứ giác BEDF có
ED//BF
ED=BF
Do đó: BEDF là hình bình hành
Suy ra: BE=DF
c: ta có: BEDF là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường
mà AC và BD cắt nhau tại trung điểm của mỗi đường
nên AC,BD,EF đồng quy
KV
16 tháng 7 2023
Bài 2
a) 3x(x - 1) - 3(x - 1) = 0
(x - 1)(3x - 3) = 0
3(x - 1)(x - 1) = 0
3(x - 1)² = 0
x - 1 = 0
x = 1
b) x² - x = 0
x(x - 1) = 0
x = 0 hoặc x - 1 = 0
*) x - 1 = 0
x = 1
Vậy x = 0; x = 1
c) 25x² - 100x = 0
25x(x - 4) = 0
25x = 0 hoặc x - 4 = 0
*) 25x = 0
x = 0
*) x - 4 = 0
x = 4
Vậy x = 0; x = 4
d) (2x - 1)² - 64 = 0
(2x - 1 - 8)(2x - 1 + 8) = 0
(2x - 9)(2x + 7) = 0
*) 2x - 9 = 0
2x = 9
x = 9/2
*) 2x + 7 = 0
2x = -7
x = -7/2
Vậy x = -7/2; x = 9/2
22 tháng 2 2022
Câu 3:
a: \(\left(x+2\right)^2=x^2+4x+4\)
b: \(\left(x+3\right)^2=x^2+6x+9\)
c: \(\left(x-3\right)^2=x^2-6x+9\)
d: \(\left(x-7\right)^2=x^2-14x+49\)
e: \(x^2-6x+9=\left(x-3\right)^2\)
f: \(x^2-8x+16=\left(x-4\right)^2\)
g: \(=\left(x-10\right)\left(x+10\right)\)
h: \(=\left(x-11\right)\left(x+11\right)\)
23 tháng 7 2021
1) Xét hình thang ADCB(AD//CB) có
M là trung điểm của AB
K là trung điểm của DC
Do đó: MK là đường trung bình của hình thang ADCB(Định nghĩa đường trung bình của tam giác)
Suy ra: MK//AD//BC và \(MK=\dfrac{AD+BC}{2}\)(Định lí 4 về đường trung bình của tam giác)
2) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
3) Ta có: MN//BC(cmt)
MK//BC(cmt)
mà MN và MK có điểm chung là M
nên M,N,K thẳng hàng(đpcm)
26 tháng 8 2021
Bài 3:
a:Ta có: \(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=-\dfrac{1}{2}\\x+\dfrac{3}{4}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
b: Ta có: \(23-\left(2x+3\right)^2=-2\)
\(\Leftrightarrow\left(2x+3\right)^2=25\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)
26 tháng 8 2021
Bài 2:
a: Ta có: \(\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
b: Ta có: \(x^3+4x=0\)
\(\Leftrightarrow x\left(x^2+4\right)=0\)
hay x=0
10 tháng 3 2022
Bài 1:
a: m<n nên m+2<n+2
b: m+2<n+2<n+4
c: 3m+4>3n+4
d: -3m+4<-3n+4
14 tháng 8 2021
bài 10
b) x3-5x-14=x(x2-5x-14)=x(x2+7x-2x-14)=x[(x2-2x)+(7x-14)]=x[x(x-2)+7(x-2)]=x(x-2)(x+7)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-2=0\\x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-7\end{matrix}\right.\)
14 tháng 8 2021
Bài 10:
c: Ta có: \(x^3-5x^2-14x\)
\(=x\left(x^2-5x-14\right)\)
\(=x\left(x-7\right)\left(x+2\right)\)
NT
giúp mình bài 1 câu g,h và bài 2 với ạ
1