
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a: \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
b: \(x+5\sqrt{x}+6=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)
c: \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
d: \(3x-6\sqrt{x}-6=3\left(x-\sqrt{x}-2\right)=3\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
Bài 3:
a) \(\sqrt{3\left(x+2\right)}=6\left(đk:x\ge-2\right)\)
\(\Leftrightarrow3\left(x+2\right)=36\)
\(\Leftrightarrow3x=30\Leftrightarrow x=10\)(thỏa đk)
b) \(\sqrt{5x^2}=x+2\left(đk:x\ge-2\right)\)
\(\Leftrightarrow5x^2=\left(x+2\right)^2\)
\(\Leftrightarrow4x^2-4x-4=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=\dfrac{5}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{\sqrt{5}}{2}\\x-\dfrac{1}{2}=-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{5}}{2}\\x=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)(thỏa đk)
c) \(\sqrt{x^2-8x+16}=x+2\left(1\right)\left(đk:x\ge-2\right)\)
\(\Leftrightarrow\sqrt{\left(x-4\right)^2}=x+2\Leftrightarrow\left|x-4\right|=x+2\)
TH1: \(x\ge4\)
\(\left(1\right)\Leftrightarrow x-4=x+2\Leftrightarrow-4=2\)(vô lý)
TH2: \(-2\le x< 4\)
\(\left(1\right)\Leftrightarrow4-x=x+2\)
\(\Leftrightarrow x=1\)(thỏa đk)
d) \(\sqrt{x^2-4x+4}-2x+5=0\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}-2x+5=0\left(2\right)\Leftrightarrow\left|x-2\right|-2x+5=0\)
TH1: \(x\ge2\)
\(\left(2\right)\Leftrightarrow x-2-2x+5=0\)
\(\Leftrightarrow x=3\)(thỏa đk)
TH2: \(\dfrac{5}{2}\le x< 2\)
\(\left(2\right)\Leftrightarrow2-x-2x+5=0\)
\(\Leftrightarrow x=\dfrac{7}{3}\)(không thỏa đk)
Bài 4:
a) \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)
b) \(x+5\sqrt{x}+6=\left(\sqrt{x}+\dfrac{5}{2}\right)^2-\dfrac{1}{4}=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)
c) \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
d) \(3x-6\sqrt{x}-6=3\left(\sqrt{x}-1-\sqrt{3}\right)\left(\sqrt{x}-1+\sqrt{3}\right)\)

bài 3
a)trong \(\Delta ABC\) vuông tại A có
\(AB^2=BC.BH\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{13^2}{5}=33,8\)
\(AC=\sqrt{BC^2-AB^2}\left(pytago\right)=\sqrt{33,8^2-13^2}=31,2\)
\(sinB=\dfrac{AC}{BC}=\dfrac{31,2}{33,8}=0,9\)
\(sinC=\dfrac{AB}{BC}=\dfrac{13}{33,8}=0,4\)
b)BC=BH+HC=3+4=7
trong \(\Delta ABC\) vuông tại A có
\(AC^2=BC.HC=7.4=28\Rightarrow AC=5,3\)
\(AB^2=BC.HC=7.3=21\Rightarrow AB=4,6\)
\(sinB=\dfrac{AC}{BC}=\dfrac{5,3}{7}=0,8\)
\(sinC=\dfrac{AB}{BC}=\dfrac{4,6}{7}=0,7\)
bài 4
a)A=\(cos^252^o.cos45^o+sin^252^o.cos45^o\)
A=\(cos45^o\left(cos^252^o+sin^252^o\right)\)
A=\(cos45^o=\dfrac{\sqrt{2}}{2}\)
b)\(B=tan60^o.cos^247^o+sin^247^o.tan60^o\)
B=\(tan60^o\left(cos^247^o+sin^247^o\right)\)
B=\(tan60^o=\sqrt{3}\)

Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông

\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)


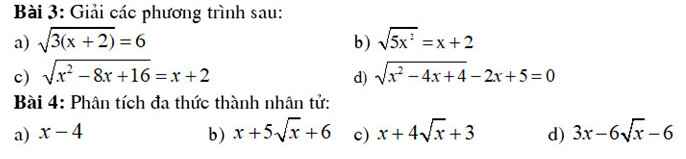





 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
3:Gọi chiều dài, chiều rộng là a,b
Chu vi là 64 nên a+b=64/2=32
Theo đề, ta có hệ:
a+b=32 và (a-2)(b+3)=ab+30
=>a+b=32 và 3a-2b=36
=>a=20 và b=12