
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\alpha\in\left(-90;0\right)\Rightarrow\left\{{}\begin{matrix}sina< 0\\cosa>0\end{matrix}\right.\) \(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{3}{5}\)
\(cot\left(a+60^0\right)=\dfrac{cos\left(a+60^0\right)}{sin\left(a+60^0\right)}=\dfrac{cosa.cos60^0-sina.sin60^0}{sina.cos60^0+cosa.sin60^0}\)
\(=\dfrac{\dfrac{3}{5}.\dfrac{1}{2}-\left(-\dfrac{4}{5}\right).\dfrac{\sqrt{3}}{2}}{-\dfrac{4}{5}.\dfrac{1}{2}+\dfrac{3}{5}.\dfrac{\sqrt{3}}{2}}=...\)
\(sin\left(45^0-a\right)=sin45^0.cosa-cos45^0.sina=\dfrac{\sqrt{2}}{2}.\dfrac{3}{5}-\dfrac{\sqrt{2}}{2}.\left(-\dfrac{4}{5}\right)=...\)


Đặt \(\sqrt{\dfrac{x^2}{x-3}}=a\left(a>=0\right)\)
Theo đề, ta có bất phương trình:
\(a^2>2a+8\)
=>(a-4)(a+2)>0
=>a-4>0
\(\Leftrightarrow\dfrac{x^2}{x-3}>16\)
\(\Leftrightarrow x^2-16x+48>0\)
\(\Leftrightarrow x\in R\)
Vậy: S=R\{3}

1b)
Song song => (d): x-y +a =0
Vì d đi qua C(2;-2) => 2- (-2)+a=0
<=>a=4
=> d: x-y+4=0


Lời giải:
a. $A=\left\{1; 2; 3; 4; 5\right\}$
$B=\left\{3; 4; 5;6 ;7\right\}$
$A\cap B=\left\{ 3; 4;5\right\}$
$A\cup B =\left\{1;2 ;3; 4; 5;6 ;7\right\}$
b.
$A\setminus B = (-2;-1)$

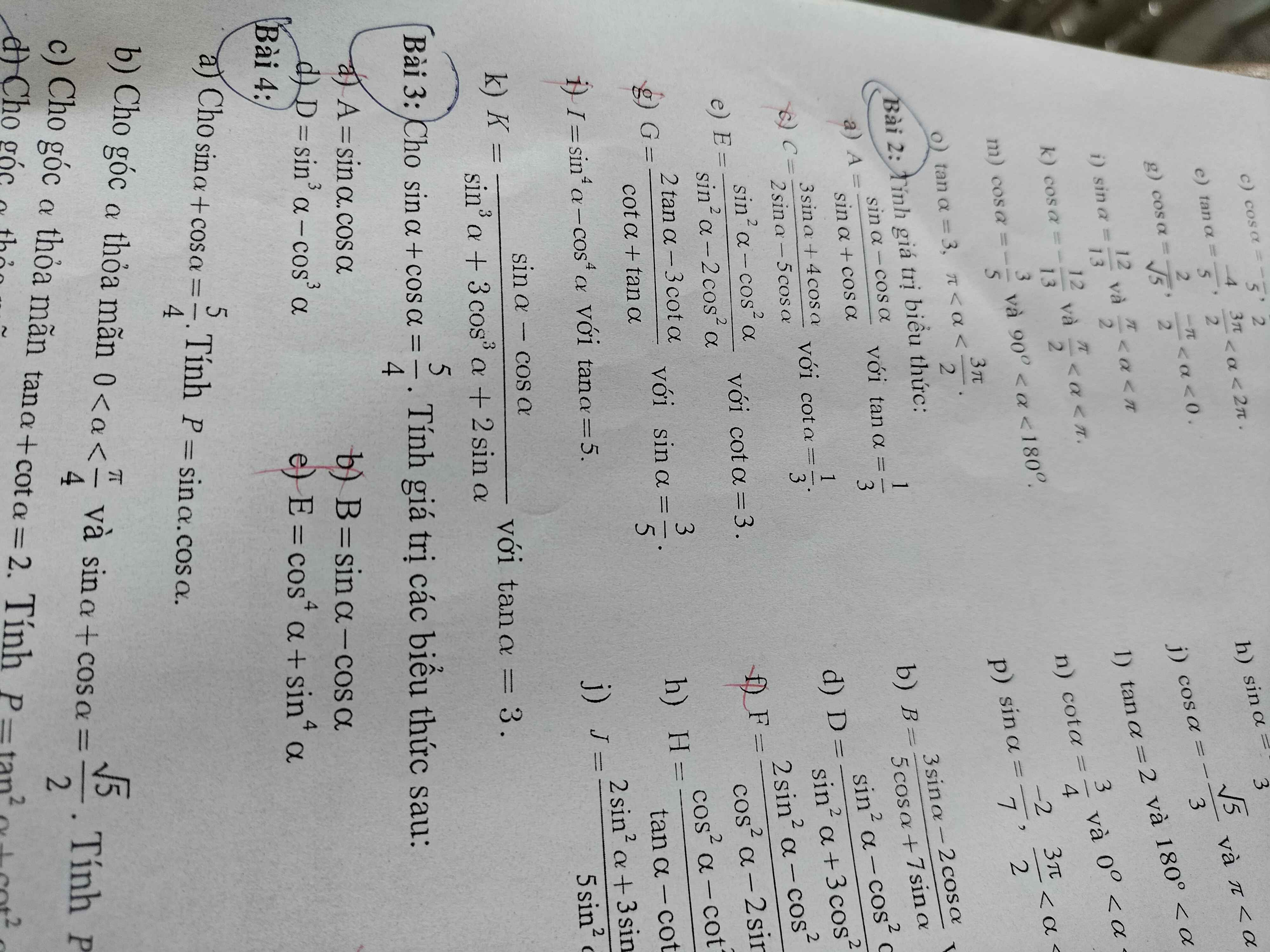

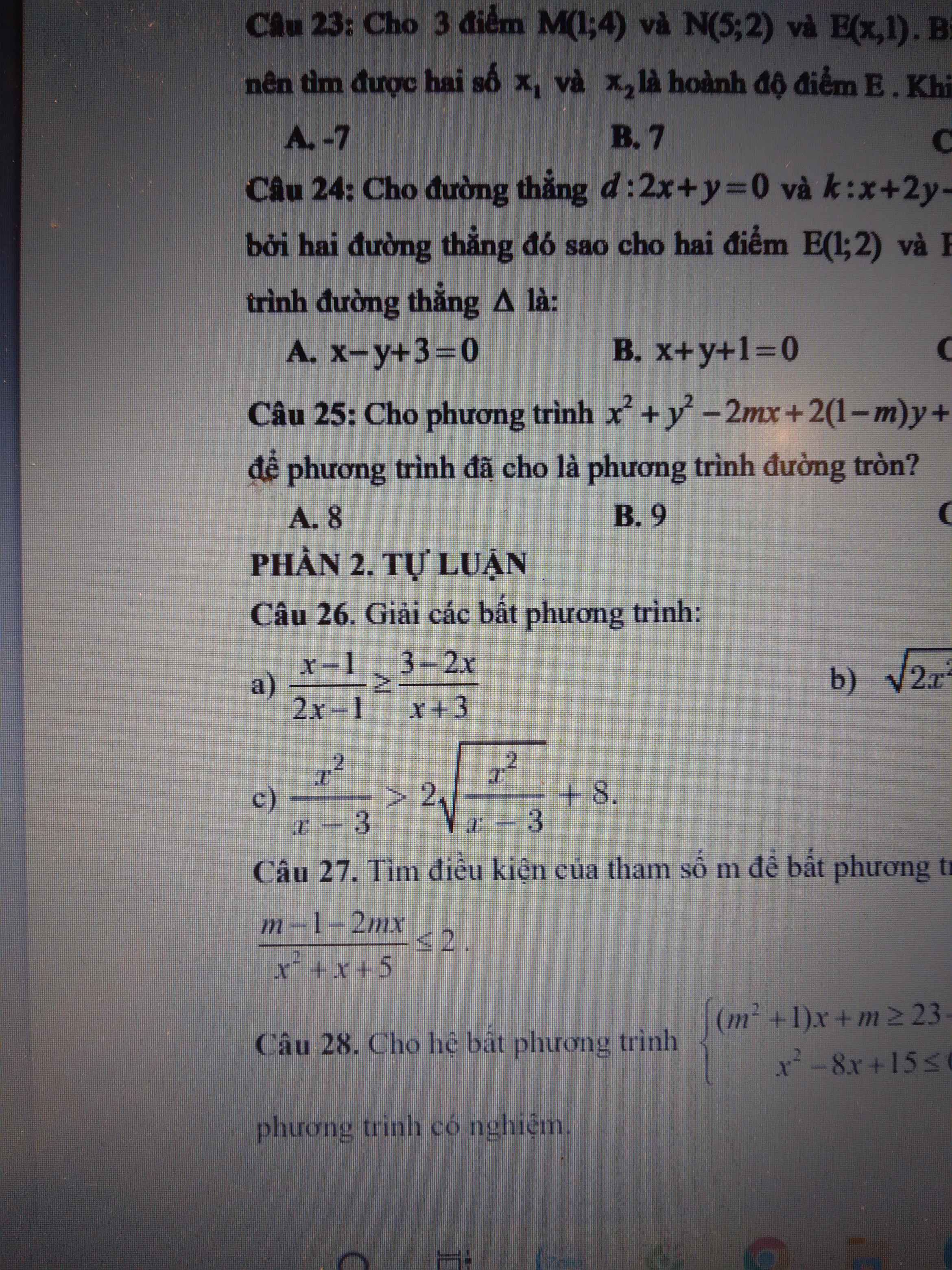



Lơ giải:
\(\frac{25}{16}=(\sin a+\cos a)^2=\sin ^2a+\cos ^2a+2\sin a\cos a=1+2\sin a\cos a\)
\(\Rightarrow \sin a\cos a=\frac{9}{32}\)
\((\sin a-\cos a)^2=(\sin a+\cos a)^2-4\sin a\cos a=\frac{25}{16}-4.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow \sin a-\cos a=\pm \frac{\sqrt{7}}{4}\)
Do đó:
\(D=\sin ^3a-\cos ^3a=(\sin a-\cos a)(\sin ^2a+\sin a\cos a+\cos ^2a)\)
\(=(\sin a-\cos a)(1+\sin a\cos a)\)
\(=\pm \frac{\sqrt{7}}{4}(1+\frac{9}{32})=\pm \frac{41\sqrt{7}}{128}\)
Lơ giải:
\(\frac{25}{16}=(\sin a+\cos a)^2=\sin ^2a+\cos ^2a+2\sin a\cos a=1+2\sin a\cos a\)
\(\Rightarrow \sin a\cos a=\frac{9}{32}\)
\((\sin a-\cos a)^2=(\sin a+\cos a)^2-4\sin a\cos a=\frac{25}{16}-4.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow \sin a-\cos a=\pm \frac{\sqrt{7}}{4}\)
Do đó:
\(D=\sin ^3a-\cos ^3a=(\sin a-\cos a)(\sin ^2a+\sin a\cos a+\cos ^2a)\)
\(=(\sin a-\cos a)(1+\sin a\cos a)\)
\(=\pm \frac{\sqrt{7}}{4}(1+\frac{9}{32})=\pm \frac{41\sqrt{7}}{128}\)