K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 1 2023
a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
5 tháng 4 2022
c: =>4(2x+2)+6>5(3x-2)
=>8x+8+6>15x-10
=>8x+14>15x-10
=>-7x>-24
hay x<24/7
d: =>3(2x+1)-5(2x-2)>225
=>6x+3-10x+10>225
=>-4x+13>225
=>-4x>212
hay x<-53
9 tháng 12 2021
a: Xét tứ giác MEDF có
\(\widehat{MED}=\widehat{MFD}=\widehat{FME}=90^0\)
Do đó: MEDF là hình chữ nhật
22 tháng 6 2023
Câu 3:
Gọi số học sinh nữ và số học sinh nam lần lượt là a,b
Tổng số điểm là 291 nên 7,8a+7,5b=291
Có 38 hs nên a+b=38
Do đó, ta có hệ:
a+b=38 và 7,8a+7,5b=291
=>a=20 và b=18
Vậy: Có 20 nữ
4:
Diện tích phòng là 6*9=54m2
Số viên gạch cần dùng là:
540000:60^2=150 viên
số thùng gạch cần dùng là;
150:4=37,5 thùng
10 tháng 1 2023
a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: \(HD=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(S_{ADHE}=6\cdot8=48\left(cm^2\right)\)
c: Để ADHE là hình vuông thì AH là phân giác của góc BAC
=>góc B=45 độ
NT
0
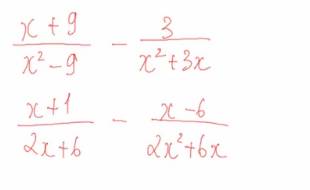
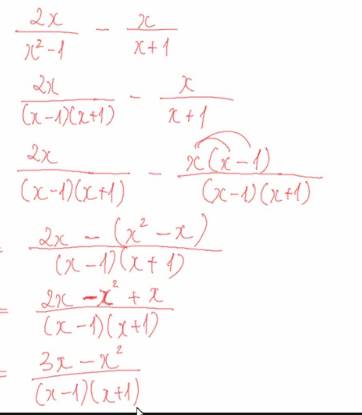
Câu 3:
a: Xét ΔBAC có \(BC^2=AB^2+AC^2\)
nên ΔBAC vuông tại A
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
mà DC>DE
nên DF>DE
Câu 4:
Đặt \(f\left(x\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Vì nghiệm của \(f\left(x\right)\) cũng là nghiệm của \(g\left(x\right)\) nên ta có:
\(\left\{{}\begin{matrix}a+b+2+1=0\\4a-2b-8+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+2b=-6\\4a-2b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-3\end{matrix}\right.\)