
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(=\dfrac{-14}{7}+\dfrac{4}{2}=-2+2=0\)
b: \(=\dfrac{1}{7}+\dfrac{6}{7}\cdot\dfrac{1}{6}=\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{2}{7}\)

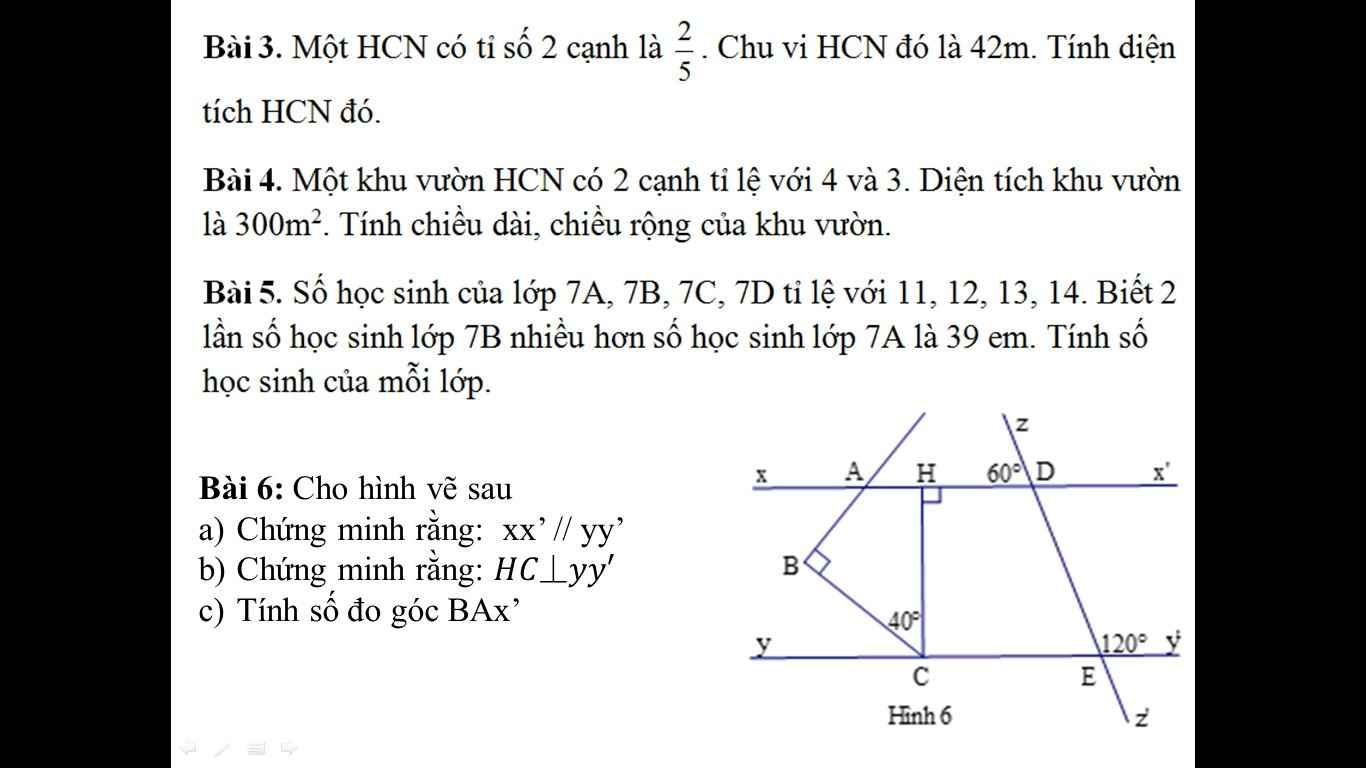
Bài 3:
Diện tích là:
\(15\cdot6=90\left(m^2\right)\)
Bài 3:
Gọi cd,cr lần lượt là a,b(m;a,b>0)
Áp dụng tc dtsbn:
\(\dfrac{b}{a}=\dfrac{2}{5}\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a+2b}{10+4}=\dfrac{42}{14}=3\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=6\end{matrix}\right.\\ \Rightarrow S_{hcn}=ab=90\left(m^2\right)\)
Bài 4:
Gọi cd,cr lân lượt là a,b(m;a,b>0)
Đặt \(\dfrac{a}{4}=\dfrac{b}{3}=k\Rightarrow a=4k;b=3k\)
\(ab=300\left(m^2\right)\\ \Rightarrow12k^2=300\\ \Rightarrow k^2=25\Rightarrow k=5\left(k>0\right)\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=15\end{matrix}\right.\)
Vậy ...
Bài 5:
Gọi số hs 7A,7B,7C,7D ll là a,b,c,d(hs;a,b,c,d∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{11}=\dfrac{b}{12}=\dfrac{c}{13}=\dfrac{d}{14}=\dfrac{2b-a}{24-11}=\dfrac{39}{13}=3\\ \Rightarrow\left\{{}\begin{matrix}a=33\\b=36\\c=39\\d=42\end{matrix}\right.\)
Vậy ...

a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔABM=ΔDBM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
c: Ta có: BA=BD
nên ΔBAD cân tại B
mà BM là đường phân giác
nên BM là đường cao
d: Ta có: ΔABM=ΔDBM
nên MA=MD
Ta có: BA=BD
nên B nằm trên đường trung trực của AD(1)
Ta có: MA=MD
nên M nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BM là đường trung trực của AD
hay BM⊥AD

\(\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x^2}{9}=\frac{y^2}{16}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{9+16}=\frac{100}{25}=4\)
Suy ra :
+) \(\frac{x}{3}=4\Rightarrow x=12\)
+) \(\frac{y}{4}=4\Rightarrow y=16\)

Bài 1.
a.
\(A=\frac{5}{4}(-8).(x^2.x)(y^2.y^2)=-10x^3y^4\)
b. $A=-10.1^3.(-1)^4=-10$
2.
\(B=\frac{15}{2}(\frac{1}{3})^2-\frac{5}{2}(\frac{1}{3})=0\)
Bài 2:
a.
$f(x)=(5x^3-2x^3)+(x^2+3x^2)-2x-3$
$=3x^3+3x^2-2x-3$
$g(x)=(2x^4-2x^4)+(-5x^3+7x^3)+(6x-4x)-1$
$=2x^3+2x-1$
b.
$f(x)+g(x)=(3x^3+3x^2-2x-3)+(2x^3+2x-1)$
$=5x^3+3x^2-4$
c.
$f(x)-g(x)=(3x^3+3x^2-2x-3)-(2x^3+2x-1)$
$=x^3+3x^2-4x-2$






 Giúp vs mn ơi !
Giúp vs mn ơi ! giúp vs mn ơi
giúp vs mn ơi
a: \(=\dfrac{-14}{7}+\dfrac{4}{2}=-2+2=0\)
b: \(=\dfrac{1}{7}+\dfrac{6}{7}\cdot\dfrac{1}{6}=\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{2}{7}\)