
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn vào you tobe bạn gõ violympic lớp 6 vòng 1 là có nha mik cũng thi vio trương mik toàn đươc điểm tối đa sắp ra vòng 5 rùi

Gọi số ngày cả ba gặp lại nhau cần tìm là x ( ngày) ( x thuộc n sao) Theo đề bài ta có: x chia hết cho 15,20,12 và x ít nhất => x = BCNN ( 15, 20,12). Ta có:
15 = 3.5
20= 2 mũ 2 . 5
12= 2 mũ 2 . 3
=> BCNN ( 15, 20, 12) = 2 mũ 2 . 3. 5 = 60
Vậy số này ít nhất cả 3 tàu gặp lại nhau là 60 ngày


a) \(\left|x\right|+2=9\Leftrightarrow\left|x\right|=7\Leftrightarrow x=\pm7\).
b) \(\left|x-4\right|=1\Leftrightarrow\orbr{\begin{cases}x-4=-1\\x-4=1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=5\end{cases}}\).

Chết đuối là nguyên nhân gây ra tử vong phổ biến nhất liên quan đến sóng lớn. Các đợt sóng trong sóng lớn và nước rút luôn hủy diệt các cấu trúc trong khu vực bị ảnh hưởng bởi các đợt sóng lên xuống. Các mối nguy hiểm khác bao gồm ngập lụt, nhiễm bẩn nước uống và hỏa hoạn từ đường dẫn ga hoặc thùng chứa vỡ.

\(A=7+7^2+7^3+7^4+7^5+7^6+7^7+7^8\)
\(A=\left(7+7^3\right)+\left(7^2+7^4\right)+\left(7^5+7^7\right)+\left(7^6+7^8\right)\)
\(A=7\cdot\left(7+7^2\right)+7^2\cdot\left(1+7^2\right)+7^5\cdot\left(1+7^2\right)+7^6\cdot\left(1+7^2\right)\)
\(A=7\cdot50+7^2\cdot50+7^5\cdot50+7^6\cdot50\)
\(A=50\cdot\left(7+7^2+7^5+7^6\right)\)
\(A=5\cdot10\cdot\left(7+7^2+7^5+7^6\right)\)
Ta có: 5 ⋮ 5
⇒ \(A=5\cdot10\cdot\left(7+7^2+7^5+7^6\right)\) ⋮ 5 (đpcm)
A = 7 + 72 + 73 + 74 + 75 + 76 + 77 + 78
A = (7 + 73) + (72+ 74) + (75 + 77) + (76 + 78)
A = 7.(1 + 72) + 72.(1 + 72) + 75.(1 + 72) + 76.(1 + 72)
A = 7.( 1 + 49) + 72.( 1 + 49) + 75.(1 + 49) + 76. (1 + 49)
A = 7.50 + 72.50 + 75.50 + 76.50
A = 50.(7 + 72 + 75 + 76)
Vì 50 ⋮ 5 nên A = 50.(7 + 72 + 76) ⋮ 5 đpcm

Ta có:C=5+52+53+...+53000
=(5+52+53)+(54+55+56)+...+(52998+52999+53000)
=5(1+5+52)+54(1+5+52)+...+52998(1+5+52)
=5(1+5+25)+54(1+5+25)+...+52998(1+5+25)
=5.31+54.31+...+52998.31
Vì 31 chia hết cho 31 nên 5.31+54.31+...+52998.31 chia hết cho 31
hay C chia hết cho 31
Vậy C chia hết cho 31.
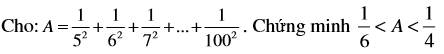
 giải giúp tui với ạ sắp đến h đi hc rùi cảm ơn nhìu
giải giúp tui với ạ sắp đến h đi hc rùi cảm ơn nhìu 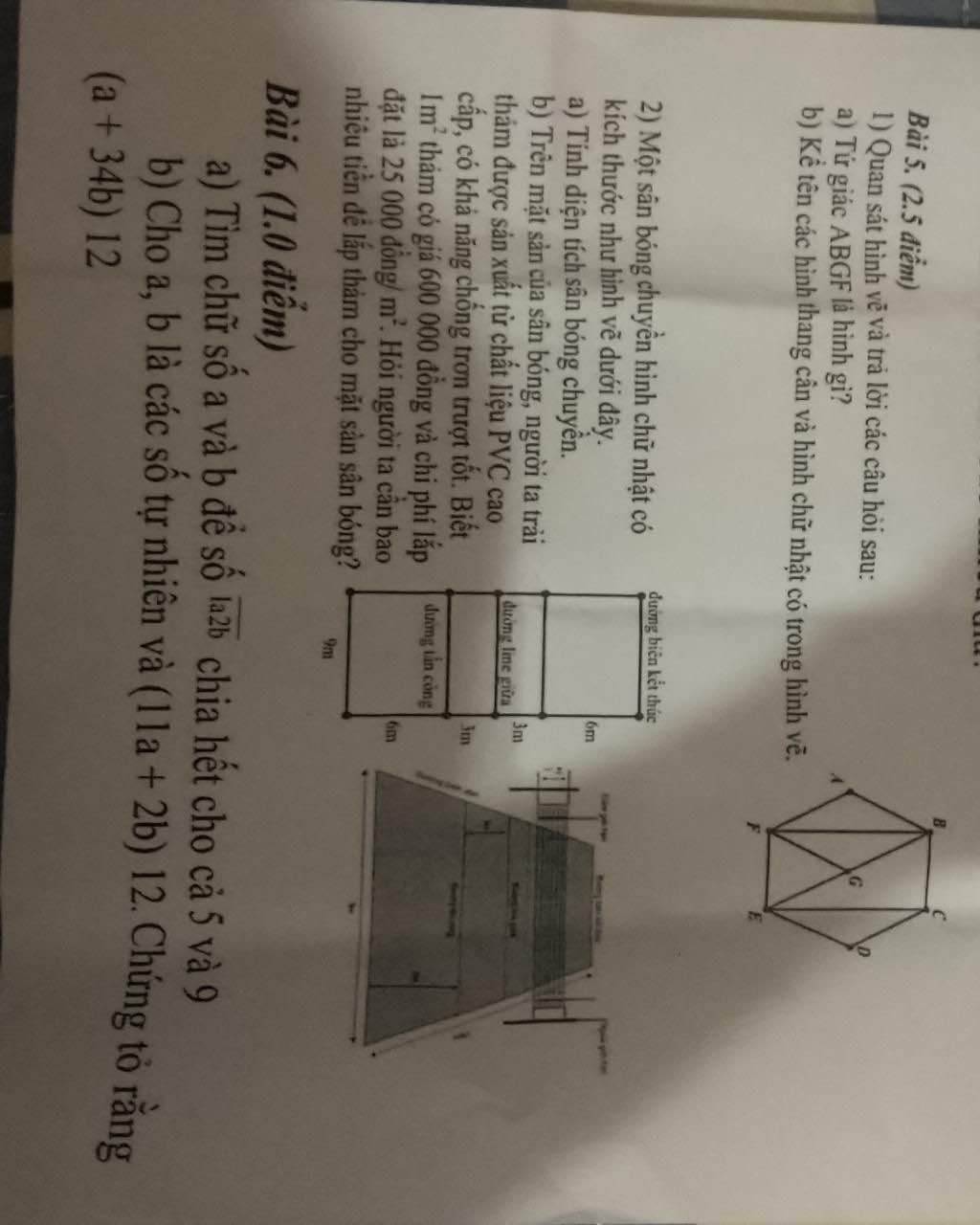
Lời giải:
$A> \frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+...+\frac{1}{100.101}$
$A> \frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{101-100}{100.101}$
$A> \frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{100}-\frac{1}{101}$
$A> \frac{1}{5}-\frac{101}>\frac{1}{6}$
---------------
$A< \frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{99.100}$
$A< \frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}$
$A< \frac{1}{4}-\frac{1}{100}< \frac{1}{4}$