
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





1.
\(\Delta'=\left(m+1\right)^2-\left(m^2+3m-7\right)=-m+8\)
Phương trình đã cho vô nghiệm khi và chỉ khi \(\Delta'< 0\)
\(\Rightarrow-m+8< 0\)
\(\Rightarrow m>8\)

2.
Do pt có 1 nghiệm bằng 2, thay \(x=2\) vào pt ta được:
\(2^2-2\left(m-1\right)-m=0\)
\(\Rightarrow6-3m=0\Rightarrow m=2\)
Khi đó nghiệm còn lại (tính theo định lý Viet là):
\(x_1x_2=-m\Rightarrow x_2=\dfrac{-m}{x_1}=\dfrac{-2}{2}=-1\)
x^2-(m-1)x-m=0 (*)
Ta có x=2 thế vào pt(*),ta có:
2^2-(m-1).2-m=0
<=> 4-2m+2-m=0
<=> -3m=-6
<=> m=2
Thế m=2 vào lại pt(*),ta lại có:
x^2-(2-1)x-2=0
<=> x^2-x-2=0
<=> x^2-2x+x-2=0
<=> (x^2-2x)+(x-2)=0
<=>x(x-2)+(x-2)=0
<=> (x-2)(x+1)=0
<=> x-2=0 hoặc x+1=0
<=>x=2 hoặc x=-1
Vậy S={−1;2}

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=1\end{matrix}\right.\)
Gọi \(x_3;x_4\) là các nghiệm của pt cần tìm, ta có:
\(\left\{{}\begin{matrix}x_3+x_4=2x_1-x_2^2+2x_2-x_1^2\\x_3x_4=\left(2x_1-x_2^2\right)\left(2x_2-x_1^2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2x_1^3-2x_2^3+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2.3-3^2+2.1=-1\\x_3x_4=4.1-2\left(3^3-3.1.3\right)+1^2=-31\end{matrix}\right.\)
Theo định lý Viet đảo, pt cần tìm có dạng:
\(x^2+x-31=0\)

1: Ta có: ΔOEF cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)EF
Xét tứ giác OIMP có \(\widehat{OIP}=\widehat{OMP}=90^0\)
nên OIMP là tứ giác nội tiếp
2: Xét ΔOMP vuông tại M có MH là đường cao
nên \(OH\cdot OP=OM^2=OF^2\)
=>\(\dfrac{OH}{OF}=\dfrac{OF}{OP}\)
Xét ΔOHF và ΔOFP có
\(\dfrac{OH}{OF}=\dfrac{OF}{OP}\)
\(\widehat{HOF}\) chung
Do đó: ΔOHF~ΔOFP






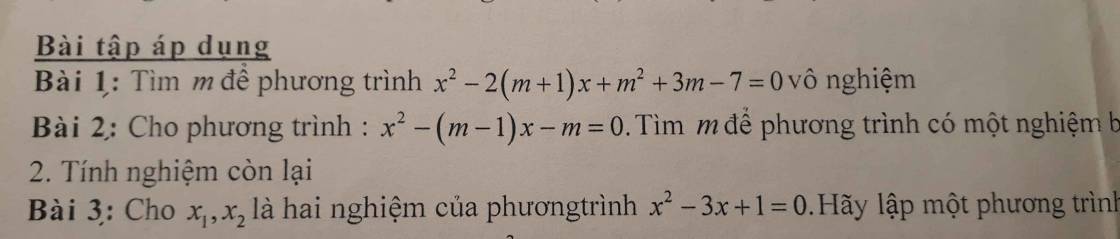
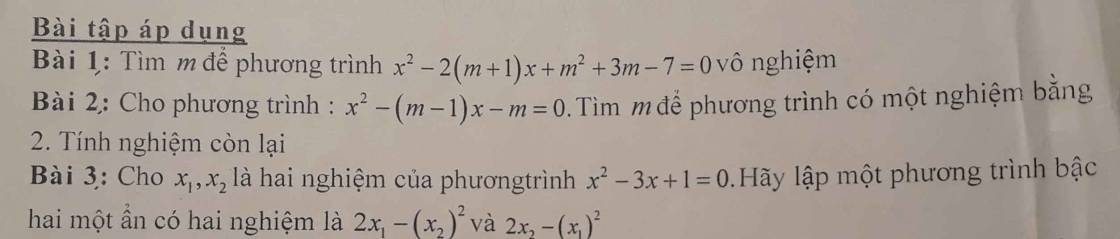
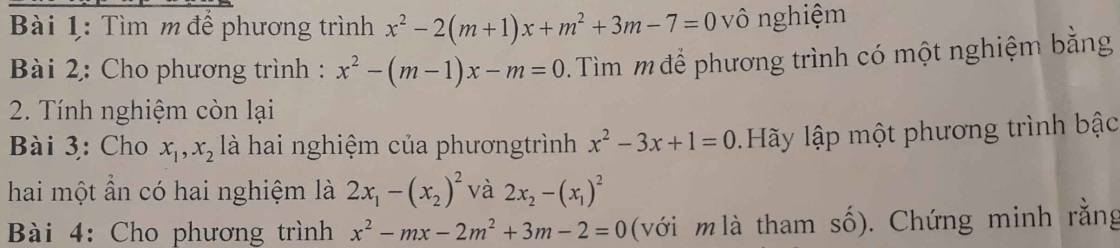



\(a,\sqrt{x^2+2x+1}-2x=1\\ \Leftrightarrow a,\left|x+1\right|=1+2x\left(x\ge-\dfrac{1}{2}\right)\\ \Leftrightarrow\left[{}\begin{matrix}x+1=1+2x\\x+1=-1-2x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-\dfrac{2}{3}\left(ktm\right)\end{matrix}\right.\)
b,ĐKXĐ:\(x\ge-2\)
\(\sqrt{x^2-8x+16}=x+2\\ \Leftrightarrow\left|x-4\right|=x+2\\ \Leftrightarrow\left[{}\begin{matrix}x-4=x+2\\x-4=-x-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}6=0\left(vô.lí\right)\\x=1\left(tm\right)\end{matrix}\right.\)
\(a,PT\Leftrightarrow\left|x+1\right|=2x+1\\ \Leftrightarrow\left[{}\begin{matrix}x+1=2x+1\left(x\ge-1\right)\\-x-1=2x+1\left(x< -1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-\dfrac{2}{3}\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=0\\ b,PT\Leftrightarrow\left|x-4\right|=x+2\\ \Leftrightarrow\left[{}\begin{matrix}x-4=x+2\left(x\ge4\right)\\4-x=x+2\left(x< 4\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x=1\left(tm\right)\end{matrix}\right.\Leftrightarrow x=1\)