
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(5\cdot2^2-18:3=5\cdot4-6=20-6=14\)
2) \(29\cdot75+25\cdot29-250=29\cdot\left(75+25\right)-250=29\cdot100-250=2900-250=2650\)
3) \(561+216+139+154=\left(561+139\right)+\left(216+154\right)=700+370=1070\)
4) \(91:\left\{350:\left[450-\left(4\cdot5^3-2^2\cdot25\right)\right]\right\}=91:\left\{350:\left[450-\left(4\cdot125-4\cdot25\right)\right]\right\}\)
\(=91:\left[350:\left(450-400\right)\right]=91:\left(350:50\right)=91:7=13\)

1/
$C=5+(5^2+5^3)+(5^4+5^5)+.....+(5^{2022}+5^{2023})$
$=5+5^2(1+5)+5^4(1+5)+....+5^{2022}(1+5)$
$=5+(1+5)(5^2+5^4+....+5^{2022})$
$=5+6(5^2+5^4+....+5^{2022})$
$\Rightarrow C$ chia $6$ dư $5$
$\Rightarrow C\not\vdots 6$
2/
$D=(1+2+2^2)+(2^3+2^4+2^5)+....+(2^{2019}+2^{2020}+2^{2021})$
$=(1+2+2^2)+2^3(1+2+2^2)+....+2^{2019}(1+2+2^2)$
$=(1+2+2^2)(1+2^3+...+2^{2019})$
$=7(1+2^3+...+2^{2019})\vdots 7$
Ta có đpcm.

a: Ư(8)={1;2;4;8}
Ư(12)={1;2;3;4;6;12}
UC(8;12)={1;2;4}
b: B(16)={0;16;32;...}
B(24)={0;24;48;...}
BC(16,24)={0;48;96;...}

Bài 1:
a. $-27+(-154)-(-27)+54$
$=(-27)-(-27)+(-154)+54=0-154+54=0-(154-54)=0-100=-100$
b.
$-35.127+(-35).(-27)+700$
$=(-35)(127-27)+700=-35.100+700=-3500+700=-2800$
c.
$-3^4-2[(-2023)^0+(-5)^2]=-81-2(1+25)=-81-2.26=-81-52$
$=-(81+52)=-133$
Bài 2:
a. $-34-2(7-x)=-10$
$2(7-x)=-34-(-10)=-24$
$7-x=-24:2=-12$
$x=7-(-12)=19$
b.
$x=ƯC(36,54,90)$
$\Rightarrow ƯCLN(36,54,90)\vdots x$
$\Rightarrow 18\vdots x$
$\Rightarrow x\in \left\{\pm 1; \pm 2; \pm 3; \pm 6; \pm 9; \pm 18\right\}$
Mà $x>5$ nên $x\in \left\{6; 9; 18\right\}$

Bài 6:
\(\Leftrightarrow6n+4⋮2n-1\)
\(\Leftrightarrow2n-1\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{1;0;4;-3\right\}\)

Lời giải:
a. Gọi 3 số tự nhiên liên tiếp là $a, a+1, a+2$. Tổng của 3 số là:
$a+(a+1)+(a+2)=3a+3=3(a+1)\vdots 3$
Ta có đpcm.
b.
Gọi 2 số chẵn liên tiếp là $2k+2$ và $2k+4$ với $k$ là số tự nhiên.
Tổng 2 số chẵn liên tiếp là:
$2k+2+2k+4=4k+6=4(k+1)+2$ chia 4 dư 2 (tức là không chia hết cho 4)
Do đó ta có đpcm.
c.
Trong 2 số tự nhiên liên tiếp luôn tồn tại 1 số chẵn và 1 số lẻ. Do đó tích của chúng sẽ luôn là số chẵn (chia hết cho 2), vì chẵn x lẻ = chẵn.
d. Gọi 3 số tự nhiên liên tiếp là $a, a+1, a+2$
Nếu $a$ chia hết cho 3 thì $a(a+1)(a+2)\vdots 3$
Nếu $a$ chia 3 dư 1 thì $a+2\vdots 3\Rightarrow a(a+1)(a+2)\vdots 3$
Nếu $a$ chia 3 dư 2 thì $a+1\vdots 3\Rightarrow a(a+1)(a+2)\vdots 3$
Vậy $a(a+1)(a+2)$ luôn chia hết cho 3 trong mọi trường hợp
Do đó ta có đpcm.

1:
a: BC=8-3=5cm
b: MN=MC+CN=1/2(CA+CB)
=1/2*AB=4cm
2:
a: Có 2 tia là OA và OB
b: AB=OB+OA=11cm
c: AC=BC=11/2=5,5cm

bài 3:
tổng số giờ đã chảy đc từ 2 vòi : 1+1=2(giờ)
tổng số phần bể đã chảy được từ 2 vòi : \(\dfrac{1}{5}+\dfrac{1}{7}=\dfrac{7}{35}+\dfrac{5}{35}=\dfrac{12}{35}\left(ph\text{ần} b\text{ể}\right)\)
nếu chảy cùng lúc mỗi giờ chảy được : \(\dfrac{12}{35}:2=\dfrac{12}{35\cdot2}=\dfrac{6}{35}\left(ph\text{ần}b\text{ể}\right)\)
bài 4:
cách 1:
độ dài đoạn AB là : \(\dfrac{3}{4}+\dfrac{9}{8}=\dfrac{18}{24}+\dfrac{27}{24}=\dfrac{45}{24}\left(m\right)\)
diện tích ABCD là : \(\dfrac{45}{27}\cdot\dfrac{4}{7}=\dfrac{15}{14}\left(m^2\right)\)
cách 2:
diện tích AEFD là : \(\dfrac{3}{4}\cdot\dfrac{4}{7}=\dfrac{3}{7}\left(m^2\right)\)
diện tích EBCF là : \(\dfrac{9}{8}\cdot\dfrac{4}{7}=\dfrac{9}{14}\left(m^2\right)\)
diện tích ABCD là : \(\dfrac{3}{7}+\dfrac{9}{14}=\dfrac{15}{14}\left(m^2\right)\)

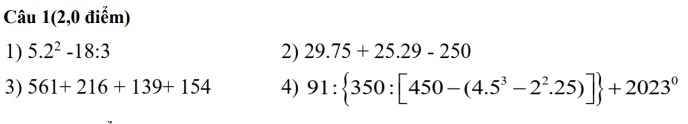
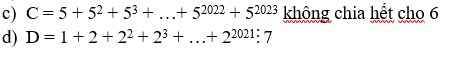
 giúp em với ạ em đang cần gấp cảm ơn ạ
giúp em với ạ em đang cần gấp cảm ơn ạ 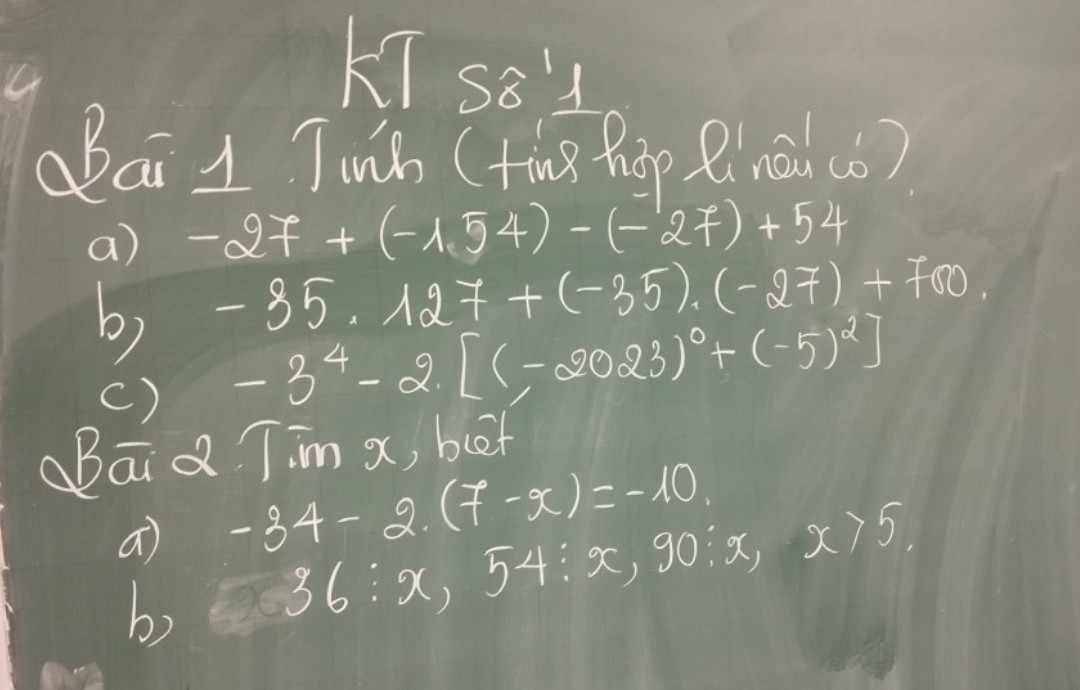
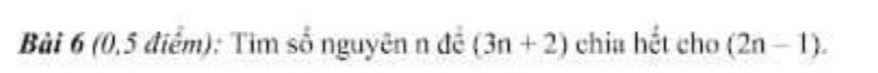 mn giúp em với ạ, em đang cần gấp lắm ạ
mn giúp em với ạ, em đang cần gấp lắm ạ



b) Diện tích hình tròn là: \(4^2.3,14=50,24\left(cm^2\right).\)
Chu vi hình tròn là: \(4.2.3,14=25,12\left(cm\right).\)
a) Ta có hình vẽ sau:
b) Diện tích hình tròn là:
4 . 4 . 3,14 = 50,24 (cm2)
Chu vi hình tròn là:
4 . 2 . 3,14 = 25,12 (cm)