DD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BG
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
\(y=\dfrac{2x-1}{x+m}\Rightarrow y'=\dfrac{2m+1}{\left(x+m\right)^2}\)
Hàm nghịch biến trên miền xác định khi:
\(2m+1< 0\Rightarrow m< -\dfrac{1}{2}\)
23 tháng 10 2019
\(x^{2019}-y^{2019}+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}\right)+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2\right)=0\)(1)
Có: \(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2>0\)mọi x, y.
(1) <=> \(x-y=0\)
<=> x = y
Thế vào P ta có:
\(P=x^4-2x^2+2=\left(x^2-1\right)^2+1\ge1\)
"=" xảy ra <=> \(y=x=\pm1\)
Vậy min P =1 khi và chỉ khi x = y =1 hoặc x = y =-1.
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2023
\(P=\left(x-y\right)+\left(y-z\right)+z+\dfrac{81}{z\left(x-y\right)\left(y-z\right)}+12\)
\(P\ge4\sqrt[4]{\left(x-y\right)\left(y-z\right).z.\dfrac{81}{z\left(x-y\right)\left(y-z\right)}}+12=24\)
\(P_{min}=24\) khi \(\left(x;y;z\right)=\left(9;6;3\right)\)
27 tháng 10
đây là những món quà mà bn sẽ nhận đc: 1: áo quần 2: tiền 3: đc nhiều người yêu quý 4: may mắn cả 5: luôn vui vẻ trong cuộc sống 6: đc crush thích thầm 7: học giỏi 8: trở nên xinh đẹp phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người,
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
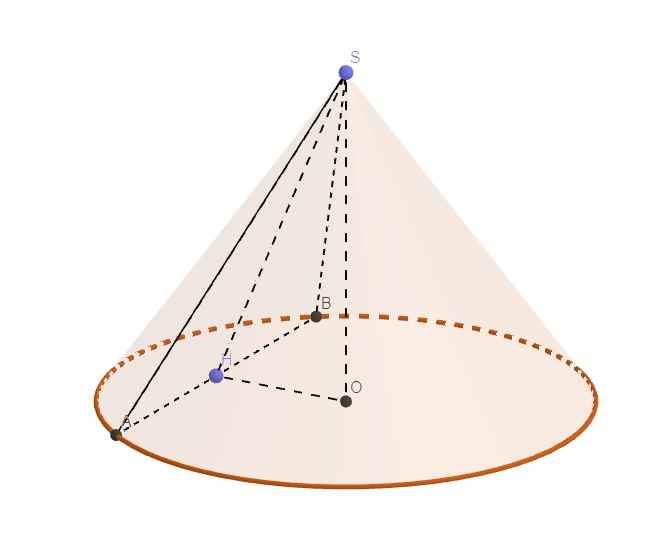
Đặt tên các điểm như hình vẽ, với H là trung điểm AB
\(\Rightarrow\widehat{SHO}=60^0\) (là góc giữa thiết diện và đáy nón)
Tam giác SAB đều \(\Rightarrow SH=\dfrac{AB\sqrt{3}}{2}=2\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow\left\{{}\begin{matrix}OH=SH.cos60^0=\sqrt{3}\\h=SO=SH.sin60^0=3\end{matrix}\right.\)
\(R=OA=\sqrt{AH^2+OH^2}=\sqrt{2^2+3}=\sqrt{7}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi.7.3=7\pi\left(cm^3\right)\)
HT
10 tháng 3 2022
Mình ko phải thầy việt lâm thì mình làm có được ko nhỉ kk :v
\(A,B\in d\Rightarrow\left\{{}\begin{matrix}A\left(t_A+2;-4t_A+1;-t_A+3\right)\\B\left(t_B+2;-4t_B+1;-t_B+3\right)\end{matrix}\right.\)
\(\overrightarrow{AM}=\left(-1-t_A;4t_A-2;-2+t_A\right);\overrightarrow{BM}=\left(-1-t_B;4t_B-2;-2+t_B\right)\)
\(\overrightarrow{AM}.\overrightarrow{BM}=0\Leftrightarrow\left(1+t_A\right)\left(1+t_B\right)+\left(4t_A-2\right)\left(4t_B-2\right)+\left(t_A-2\right)\left(t_B-2\right)=0\)
\(\left|\overrightarrow{AM}\right|=\left|\overrightarrow{BM}\right|\Leftrightarrow\left(t_A+1\right)^2+\left(4t_A-2\right)^2+\left(t_A-2\right)^2=\left(t_B+1\right)^2+\left(4t_B-2\right)^2+\left(t_B-2\right)^2\)
hệ phương trình 2 ẩn, đến đây là việc của bạn r :v
AH
Akai Haruma
Giáo viên
31 tháng 1 2017
Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
hàm số \(y=x^0\text{ cũng chính là đường thẳng }y=1\) đây là một đường thẳng vuông góc với trục Oy tại điểm (0,1) thôi
còn hàm \(y=\frac{1}{x}\Rightarrow y'=-\frac{1}{x^2}< 0\forall x\) nên hàm số nghịch biến trên R.
Đồ thị hàm số