
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(128+\left(-5\right).12+\left(-68\right):\left(-17\right)=128+\left(-60\right)+4=68+4=72\)
\(128+\left(-5\right)\cdot12+\left(-68\right):\left(-17\right)\)
\(=128+\left(-60\right)+4=68+4=72\)

\(\dfrac{x-13}{87}-1+\dfrac{x-27}{73}-1+\dfrac{x-67}{33}-1+\dfrac{x-73}{27}-1=0\)
\(\Leftrightarrow\dfrac{x-100}{87}+\dfrac{x-100}{73}+\dfrac{x-100}{33}+\dfrac{x-100}{27}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{87}+\dfrac{1}{73}+\dfrac{1}{33}+\dfrac{1}{27}\ne0\right)=0\Leftrightarrow x=100\)

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm

\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)

\(\left(x-1\right)-7=4\left(-1-x\right)\\ -7x+7=-4-4x\\ -7x-7+4+4x=0\\ -3x-3=0\\ -3\left(x-1\right)=0\\ x-1=0\\ x=1\)

a)\(-1,6:\left(1+\dfrac{2}{3}\right)=-1,6:\dfrac{5}{3}=-\dfrac{8}{5}.\dfrac{3}{5}=\dfrac{-24}{25}\)
b)\(\left(\dfrac{-2}{3}\right)+\dfrac{3}{4}-\left(-\dfrac{1}{6}\right)+\left(\dfrac{-2}{5}\right)=-\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{1}{6}-\dfrac{2}{5}=\dfrac{-40+45+10-24}{60}=\dfrac{-9}{60}=\dfrac{-3}{20}\)
c)\(\left(\dfrac{-3}{7}:\dfrac{2}{11}+\dfrac{-4}{7}:\dfrac{2}{11}\right).\dfrac{7}{33}=\left(\dfrac{-3}{7}.\dfrac{11}{2}+\dfrac{-4}{7}.\dfrac{11}{2}\right).\dfrac{7}{33}=\left[\dfrac{11}{2}\left(\dfrac{-3}{7}+\dfrac{-4}{7}\right)\right].\dfrac{7}{33}=\dfrac{-11}{2}.\dfrac{7}{33}=\dfrac{-7}{6}\)
d)\(\dfrac{-5}{8}+\dfrac{4}{9}:\left(\dfrac{-2}{3}\right)-\dfrac{7}{20}.\left(\dfrac{-5}{14}\right)=\dfrac{-5}{8}-\dfrac{4}{9}.\dfrac{3}{2}+\dfrac{1}{8}=\dfrac{-5}{8}+\dfrac{1}{8}-\dfrac{2}{3}=-\dfrac{7}{6}\)

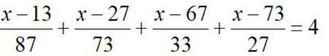
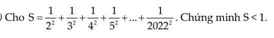
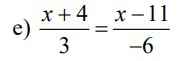
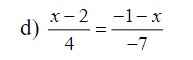
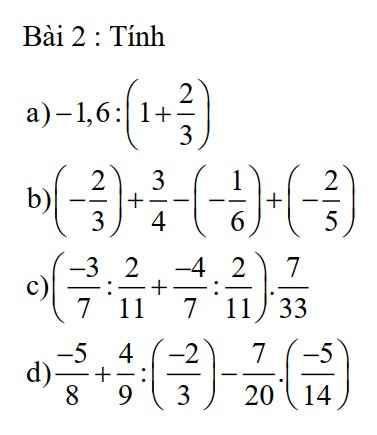 giúp với giúp với giúp e với ạ. e cảm ơn
giúp với giúp với giúp e với ạ. e cảm ơn
a: Để A là phân số thì \(n+1\ne0\)
=>\(n\ne-1\)
b: \(n^2-1=0\)
=>\(n^2=1\)
=>\(\left[{}\begin{matrix}n=1\left(nhận\right)\\n=-1\left(loại\right)\end{matrix}\right.\)
Thay n=1 vào A, ta được:
\(A=\dfrac{3\cdot1-1}{1+1}=\dfrac{3-1}{2}=1\)
c: Để A là số nguyên thì \(3n-1⋮n+1\)
=>\(3n+3-4⋮n+1\)
=>\(-4⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)
d: \(A=\dfrac{3n-1}{n+1}=\dfrac{3n+3-4}{n+1}=3-\dfrac{4}{n+1}\)
Để A min thì \(\dfrac{-4}{n+1}\) min
=>n+1 là số nguyên dương nhỏ nhất
=>n+1=1
=>n=0
=>\(A=3-\dfrac{4}{0+1}=3-4=-1\)