K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 1
a: \(\dfrac{2}{x+5}=\dfrac{2\cdot4\cdot\left(x-5\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{8\left(x-5\right)}{4\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{-3}{4x-20}=\dfrac{-3}{4\left(x-5\right)}=\dfrac{-3\left(x+5\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{-3x-15}{4\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{-x+2}{x^2-25}=\dfrac{-x+2}{\left(x-5\right)\left(x+5\right)}=\dfrac{4\left(-x+2\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{-4x+8}{4\left(x-5\right)\left(x+5\right)}\)
b: \(\dfrac{1}{3x-6y}=\dfrac{1}{3\left(x-2y\right)}=\dfrac{\left(x-2y\right)\left(x+2y\right)}{3\left(x-2y\right)^2\cdot\left(x+2y\right)}\)
\(\dfrac{-x}{x^2-4y^2}=\dfrac{-x}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{-x\cdot3\cdot\left(x-2y\right)}{3\left(x-2y\right)^2\cdot\left(x+2y\right)}\)
\(\dfrac{-2y^2}{x^2-4xy+4y^2}=\dfrac{-2y^2}{\left(x-2y\right)^2}=\dfrac{-2y^2\cdot3\left(x+2y\right)}{3\left(x+2y\right)\left(x-2y\right)^2}\)
\(=\dfrac{-6y^2\left(x+2y\right)}{3\left(x+2y\right)\left(x-2y\right)^2}\)
24 tháng 10 2023
`#3107.101107`
2.
a)
`(x - 2y)^2 = x^2 - 2*x*2y + (2y)^2 = x^2 - 4xy + 4y^2`
`=> -2xy -> -4xy`
b)
`(4a + 3b)^2 = (4a)^2 + 2*4a*3b + (3b)^2 = 16a^2 + 24ab + 9b^2`
`=>` `a^2 -> 16a^2`; `b^2 -> 9b^2`
c)
`9x^2 + 6xy + y^2 = (3x)^2 + 2*3x*y + y^2 = (3x + y)^2`
`=>` `(3x - y)^2 -> (3x + y)^2`
d)
`(a - 2b)^3 = a^3 - 3*a^2*2b + 3*a*(2b)^2 - (2b)^3 = a^3 - 6a^2b + 12ab^2 - 8b^3`
`=>` `-8a^2b -> -6a^2b`; `6ab^2 -> 12ab^2.`
24 tháng 10 2023
Sử dụng các HĐT:
1) \(\left(A+B\right)^2=A^2+2AB+B^2\)
2) \(\left(A-B\right)^2=A^2-2AB+B^2\)
3) \(\left(A-B\right)^3=A^3-3A^2B+3AB^2-B^3\)
Làm bài này bạn chú ý cả 2 vế xem có phân tích được ra HĐT hoặc chỉnh ntnao cho đúng vs HĐT nha :v.
7 tháng 8 2021
a) Ta có: \(\left(x-1.5\right)^6+2\left(1.5-x\right)^2=0\)
\(\Leftrightarrow\left(x-1.5\right)^2\left[\left(x-1.5\right)^4+2\right]=0\)
\(\Leftrightarrow x-1.5=0\)
hay x=1,5
b) Ta có: \(2x^3+3x^2+2x+3=0\)
\(\Leftrightarrow\left(2x+3\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow2x+3=0\)
hay \(x=-\dfrac{3}{2}\)
10 tháng 12 2021
Bài 33:
a: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)
AH
Akai Haruma
Giáo viên
26 tháng 12 2023
3d.
$(2x+5)^2=9x^2$
$\Leftrightarrow (2x+5)^2-(3x)^2=0$
$\Leftrightarrow (2x+5-3x)(2x+5+3x)=0$
$\Leftrightarrow (-x+5)(5x+5)=0$
$\Leftrightarrow -x+5=0$ hoặc $5x+5=0$
$\Leftrightarrow x=5$ hoặc $x=-1$
AH
Akai Haruma
Giáo viên
26 tháng 12 2023
3b.
$x(x-2023)-2x+4046=0$
$\Leftrightarrow x(x-2023)-2(x-2023)=0$
$\Leftrightarrow (x-2023)(x-2)=0$
$\Leftrightarrow x-2023=0$ hoặc $x-2=0$
$\Leftrightarrow x=2023$ hoặc $x=2$
3c.
$x^2+5x+\frac{25}{4}=0$
$\Leftrightarrow x^2+2.x.\frac{5}{2}+(\frac{5}{2})^2=0$
$\Leftrightarrow (x+\frac{5}{2})^2=0$
$\Leftrightarrow x+\frac{5}{2}=0$
$\Leftrightarrow x=\frac{-5}{2}$
15 tháng 9 2021
\(A=\left(x-3\right)^2-\left(2x+1\right)^2\)
\(=\left(x-3-2x-2\right)\left(x-3+2x+1\right)\)
\(=-\left(x+5\right)\left(3x-2\right)\)
12 tháng 1 2022
Câu 18: B
Câu 19: B
Câu 20: D
Câu 21; D
Câu 22: B
Câu 23: B
Câu 24: A
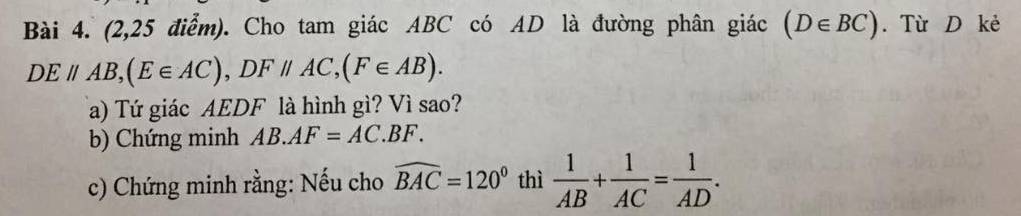
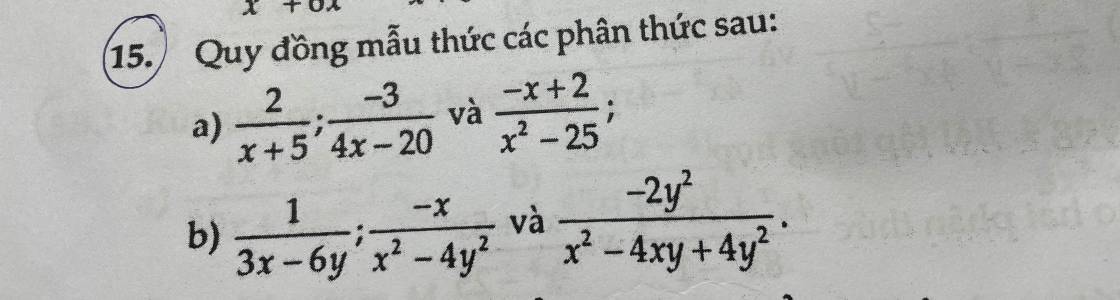
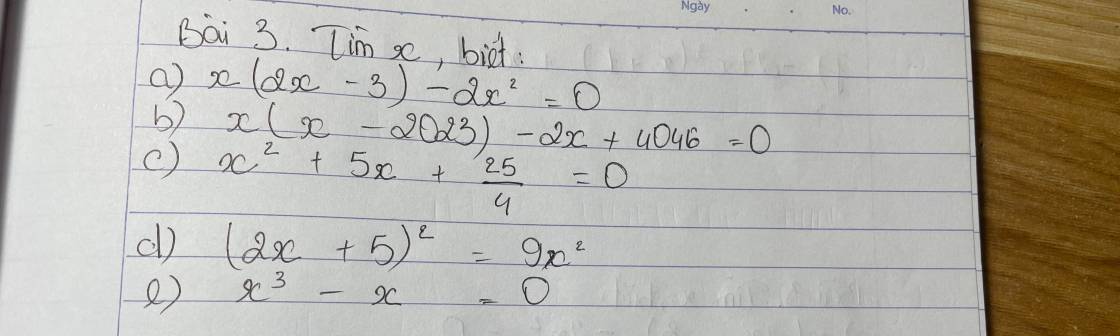
a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
Hình bình hành AEDF có AD là phân giác của góc EAF
nên AEDF là hình thoi
b: Xét ΔBAC có AD là phân giác
nên \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\left(1\right)\)
Xét ΔBAC có DF//AC
nên \(\dfrac{BD}{DC}=\dfrac{BF}{FA}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{AB}{AC}=\dfrac{BF}{FA}\)
=>\(AB\cdot AF=BF\cdot AC\)