Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-3x-4=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(4;16\right);\left(-1;1\right)\right\}\)



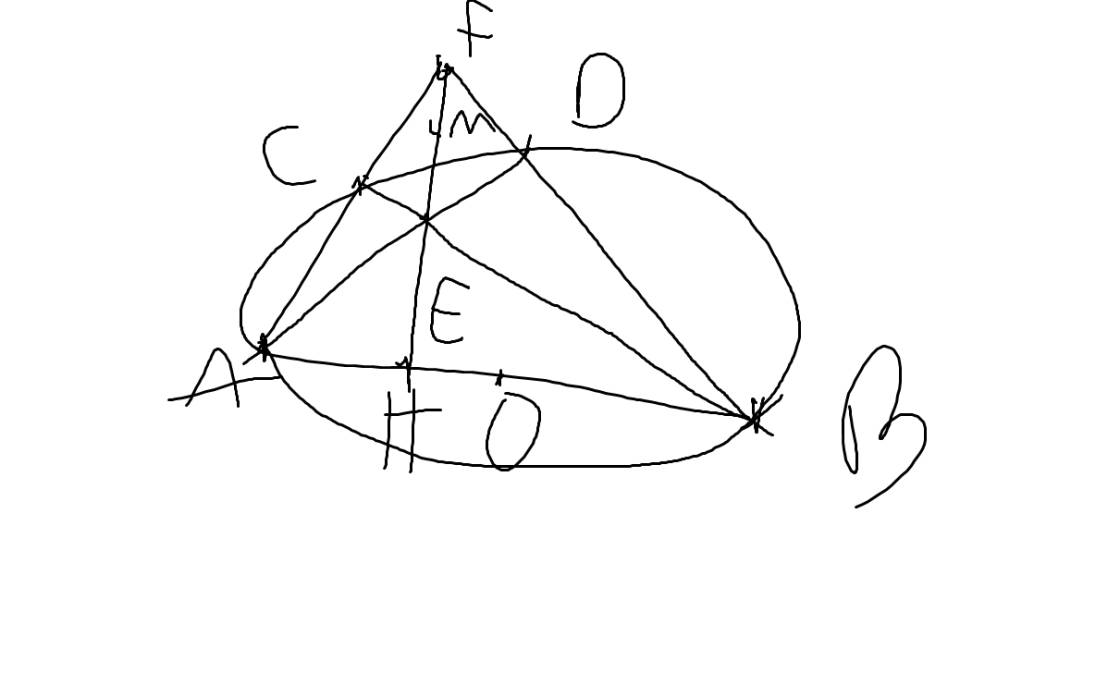
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn

Đường thẳng // với Ox và cắt Oy tại tung độ là 6 có phương trình: y = 6
Tọa độ A là nghiệm của hệ
\(\hept{\begin{cases}y=x\\y=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=6\end{cases}}\)
=> A(6, 6)
Tọa độ B là nghiệm của hệ
\(\hept{\begin{cases}y=3x\\y=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\end{cases}}\)
=> B(2, 6)

Câu 7:
b: Tọa độ của C là:
\(\left\{{}\begin{matrix}2x-3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow C\left(4;5\right)\)

b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)