giúp e vs 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp e đi em xin mng đấy ạ
24 tháng 10 2021
\(1,=\left(x-3\right)^2\\ 2,=\left(5+x\right)^2\\ 3,=\left(\dfrac{1}{2}x+2b\right)^2\\ 4,=\left(\dfrac{1}{3}-y^4\right)^2\\ 5,=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ 6,=\left(2y-5\right)\left(4y^2+10y+25\right)\\ 7,=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\\ 8,=\left(x-5\right)^2\\ 9,=8\left(x^3-\dfrac{1}{64}\right)=8\left(x-\dfrac{1}{4}\right)\left(x^2+\dfrac{1}{4}x+\dfrac{1}{16}\right)\)
MA
2
23 tháng 12 2021
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
23 tháng 12 2021
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
DM
1
8 tháng 11 2021
Bài 1:
\(a,\dfrac{25}{14x^2y}=\dfrac{75y^4}{42x^2y^5};\dfrac{14}{21xy^5}=\dfrac{28x}{42x^2y^5}\\ b,\dfrac{3x+1}{12xy^4}=\dfrac{3x\left(3x+1\right)}{36x^2y^4};\dfrac{y-2}{9x^2y^3}=\dfrac{4y\left(y-2\right)}{36x^2y^4}\\ c,\dfrac{1}{6x^3y^2}=\dfrac{6y^2}{36x^3y^4};\dfrac{x+1}{9x^2y^4}=\dfrac{4x\left(x+1\right)}{36x^3y^4};\dfrac{x-1}{4xy^3}=\dfrac{9x^2y\left(x-1\right)}{36x^3y^4}\\ d,\dfrac{3+2x}{10x^4y}=\dfrac{12y^4\left(3+2x\right)}{120x^4y^5};\dfrac{5}{8x^2y^2}=\dfrac{75x^2y^3}{120x^4y^5};\dfrac{2}{3xy^5}=\dfrac{80x^3}{120x^4y^5}\)
NT
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 12 2023
câu a, \(\dfrac{x}{x+1}\); \(\dfrac{x^2}{1-x}\); \(\dfrac{1}{x^2-1}\) (đk \(x\)≠ -1; 1)
\(x^2\) - 1 = ( \(x\) - 1).(\(x\) + 1)
\(\dfrac{x}{x+1}\) = \(\dfrac{x.\left(x-1\right)}{\left(x+1\right).\left(x-1\right)}\);
\(\dfrac{x^2}{1-x}\) = \(\dfrac{-x^2}{x-1}\)= \(\dfrac{-x^2.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{1}{x^2-1}\) = \(\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)
b, \(\dfrac{10}{x+2}\); \(\dfrac{5}{2x-4}\); \(\dfrac{1}{6-3x}\) (đk \(x\) ≠ -2; 2)
2\(x-4\) = 2.(\(x\) - 2); 6 - 3\(x\) = - 3.(\(x\) - 2)
\(\dfrac{10}{x+2}\) = \(\dfrac{10.2.3\left(x-2\right)}{2.3\left(x+2\right)\left(x-2\right)}\) = \(\dfrac{60\left(x-2\right)}{6\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{5}{2x-4}\) = \(\dfrac{5.3\left(x+2\right)}{2.3\left(x-2\right).\left(x+2\right)}\) = \(\dfrac{15.\left(x+2\right)}{6.\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{1}{6-3x}\) = \(\dfrac{-1}{3.\left(x-2\right)}\) = \(\dfrac{-1.\left(x+2\right)}{3.2.\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-2.\left(x+2\right)}{6.\left(x-2\right).\left(x+2\right)}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 12 2023
c, \(\dfrac{x}{2x-4}\); \(\dfrac{1}{2x+4}\) và \(\dfrac{3}{4-x^2}\) đk \(x\) ≠ 2; -2
\(\dfrac{x}{2x-4}\) = \(\dfrac{x}{2.\left(x-2\right)}\) = \(\dfrac{x.\left(x+2\right)}{2.\left(x-2\right).\left(x+2\right)}\)
\(\dfrac{1}{2x+4}\) = \(\dfrac{1}{2.\left(x+2\right)}\) = \(\dfrac{\left(x-2\right)}{2.\left(x+2\right).\left(x-2\right)}\)
\(\dfrac{3}{4-x^2}\) = \(\dfrac{-3}{\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-6}{2.\left(x-2\right)\left(x+2\right)}\)
MA
4
14 tháng 11 2021
Bài 6
\(a,ĐK:x\ne\pm5\\ b,P=\dfrac{x-5+2x+10-2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x+5}\\ c,P=-3\Leftrightarrow\dfrac{1}{x+5}=-3\Leftrightarrow-3\left(x+5\right)=1\Leftrightarrow x=-\dfrac{16}{3}\\ \Leftrightarrow Q=\left(3x-7\right)^2=\left[3\cdot\left(-\dfrac{16}{3}\right)-7\right]^2=529\)
14 tháng 11 2021
Bài 7:
\(a,ĐK:x\ne\pm3\\ b,P=\dfrac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\\ b,P=4\Leftrightarrow4\left(x-3\right)=4\Leftrightarrow x=4\)
HN
0
6 tháng 3 2022
a) Xét tam giác HQI:
QE là phân giác \(\widehat{Q}\left(gt\right).\)
\(\Rightarrow\dfrac{HE}{EI}=\dfrac{HQ}{QI}\) (Tính chất phân giác).
\(\Rightarrow\dfrac{HE}{EI+HE}=\dfrac{HQ}{QI+HQ}.\)
\(\Rightarrow\dfrac{HE}{HI}=\dfrac{HQ}{QI+HQ}.\)
Thay: \(\dfrac{HE}{17}=\dfrac{8}{15+8}.\)
\(\Rightarrow HE=\dfrac{136}{23}\left(cm\right).\\ \Rightarrow EI=\dfrac{255}{23}\left(cm\right).\)
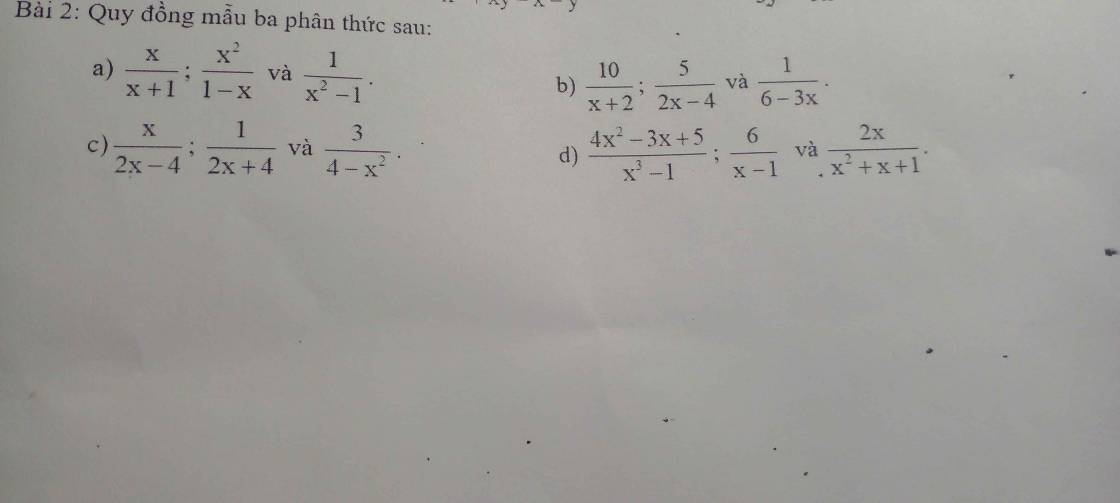
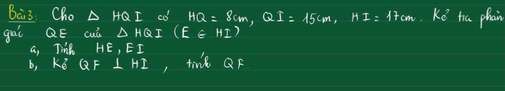
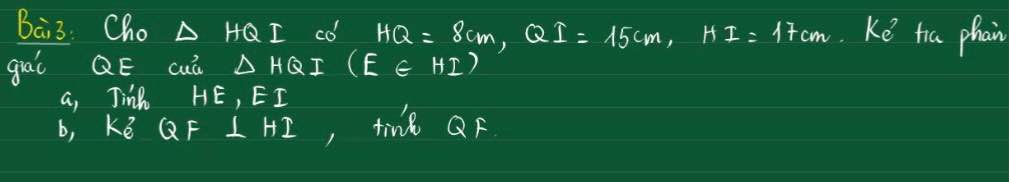
1: \(\left(x+2y\right)^2=x^2+4xy+4y^2\)
2: \(\left(2x+3y\right)^2=4x^2+12xy+9y^2\)
3: \(\left(3x-2y\right)^2=9x^2-12xy+4y^2\)
Áp dụng hằng đẳng thức đáng nhớ:
1. (a + b)2 = a2 + 2ab + b2
2. (a - b)2 = a2 - 2ab + b2
3. a2 - b2 = (a + b)(a - b)
4. (a + b)3 = a3 + 3a2b + 3ab2 + b3
5. (a - b)3 = a3 - 3a2b + 3ab2 - b3
6. a3 + b3 = (a + b)(a2 - ab + b2)
7. a3 - b3 = (a - b)(a2 + ab + b2)