Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5: \(=4b^2-2b+\dfrac{1}{4}-\dfrac{1}{4}+a-a^2\)
\(=\left(2b\right)^2-2\cdot2b\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\left(a^2-a+\dfrac{1}{4}\right)\)
\(=\left(2b-\dfrac{1}{2}\right)^2-\left(a-\dfrac{1}{2}\right)^2\)
\(=\left(2b-\dfrac{1}{2}-a+\dfrac{1}{2}\right)\left(2b-\dfrac{1}{2}+a-\dfrac{1}{2}\right)\)
\(=\left(2b-a\right)\left(2b+a-1\right)\)
6:
\(=b^2-4b+4-9c^2\)
\(=\left(b-2\right)^2-9c^2\)
\(=\left(b-2-3c\right)\left(b-2+3c\right)\)

Hình bạn vẽ hai đường chéo và chúng cắt nhau tại trung điểm của mỗi đường và vuông góc nhé.
Ta có: ABCD là hình thoi => \(AC\perp BD\)
\(AC\cap BD=\left\{O\right\}\)
Xét △AOB có:
\(AB^2=AO^2+OB^2\left(Pytago\right)\)
\(\Rightarrow AB^2=7^2+11^2\)
\(\Rightarrow AB=\sqrt{7^2+11^2}\approx13\left(cm\right)\)

Lời giải:
Áp dụng định lý Menelaus cho tam giác $CNB$ có $A,M,D$ thẳng hàng:
$\frac{DC}{DB}.\frac{MN}{MC}.\frac{AB}{AN}=1$
Mà $M$ là trung điểm $CN$ nên $MM=MC$
$\Rightarrow \frac{DC}{DB}.\frac{AB}{AN}=1$
$\Leftrightarrow \frac{AB}{AN}=\frac{DB}{DC}$ (đpcm)

Refer
Hệ quả của định lí Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.

a) Độ dài đường cao \(h\):
\(SinB=\dfrac{h}{AB}\Rightarrow h=AB.sin60^o=\dfrac{a\sqrt[]{2}}{2}\left(cm\right)\)
b) Nửa chu vi tam giác đó :
\(p=\dfrac{a+a+a}{2}=\dfrac{3a}{2}\)
Diện tích tam giác :
\(S=\sqrt[]{p\left(p-a\right)\left(p-a\right)\left(p-a\right)}\)
\(\Rightarrow S=\sqrt[]{p\left(p-a\right)^3}\)
\(\Rightarrow S=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{3a}{2}-a\right)^3}=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{a}{2}\right)^3}=\sqrt[]{\dfrac{3a^4}{16}}=\dfrac{a^2\sqrt[]{3}}{4}\)
a:Gọi tam giác đề bài cho là ΔABC đều có AH là đường cao
=>H là trung điểm của BC
=>HB=HC=a/2
AH=căn AB^2-AH^2
=a*căn 3/2
b: S ABC=1/2*AH*BC
=a^2*căn 3/4

a: Ta có: \(\left(x+3\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)=6\)
\(\Leftrightarrow x^2-9-x^2-3x+10=6\)
\(\Leftrightarrow-3x=5\)
hay \(x=-\dfrac{5}{3}\)
c: \(4x^2-9=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
\(a,\Leftrightarrow x^2-9-x^2-3x+10=6\\ \Leftrightarrow-3x=5\Leftrightarrow x=-\dfrac{5}{3}\\ b,\Leftrightarrow2x^2+3x^2-3=5x^2+5x\\ \Leftrightarrow5x=-3\Leftrightarrow x=-\dfrac{3}{5}\\ c,\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\\ d,\Leftrightarrow\left(5-2x\right)^2-4=0\\ \Leftrightarrow\left(5-2x-2\right)\left(5-2x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{7}{2}\end{matrix}\right.\\ e,\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
\(f,\Leftrightarrow\left(2x+9\right)\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{9}{2}\end{matrix}\right.\\ g,\Leftrightarrow\left(x^2-4\right)\left(3x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\\ h,\Leftrightarrow\left(x+1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x^4+2x^2+1-x^2\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x^2+x+1\right)\left(x^2-x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(vô.lí\right)\\\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow x=-1\)
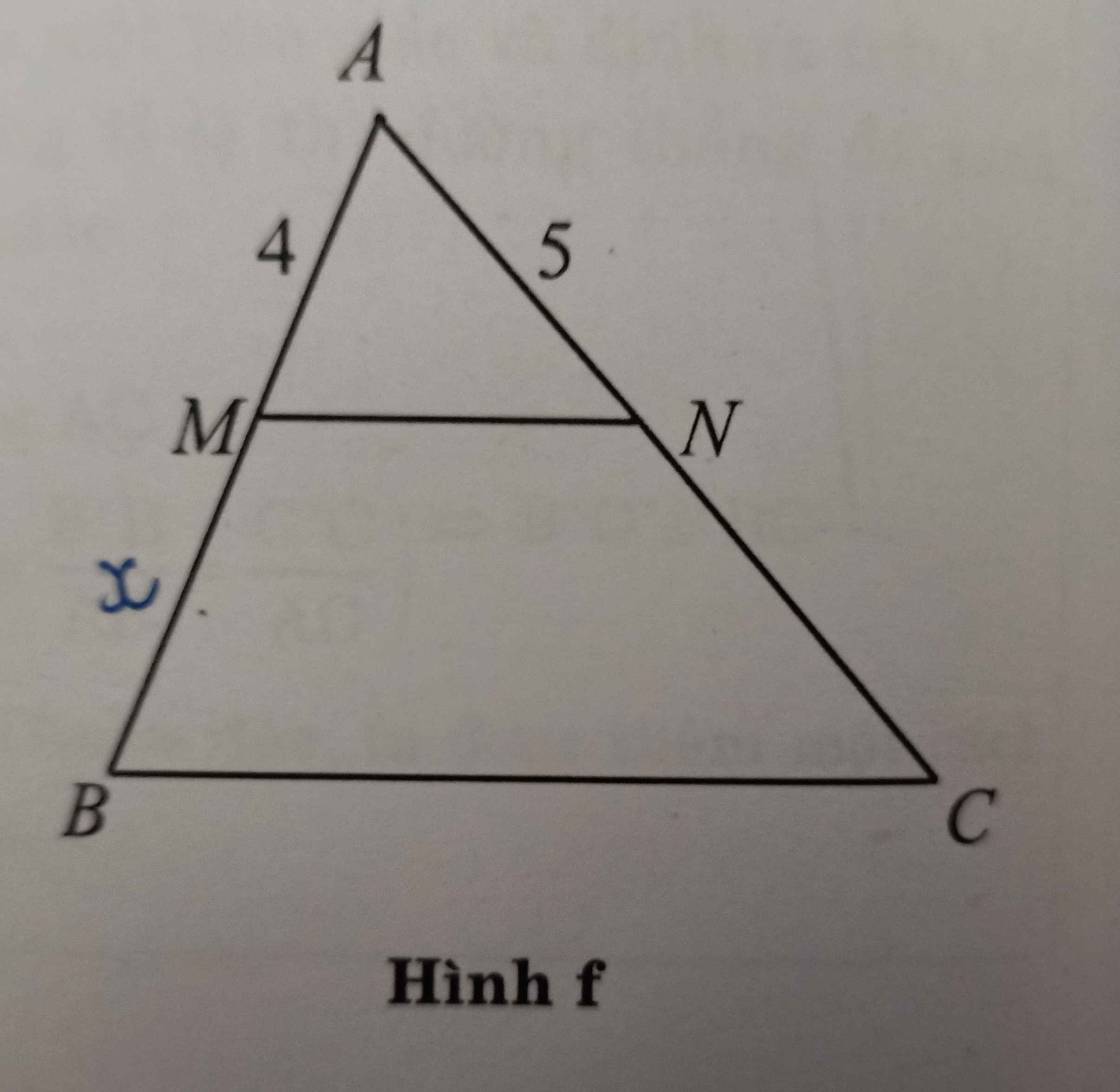
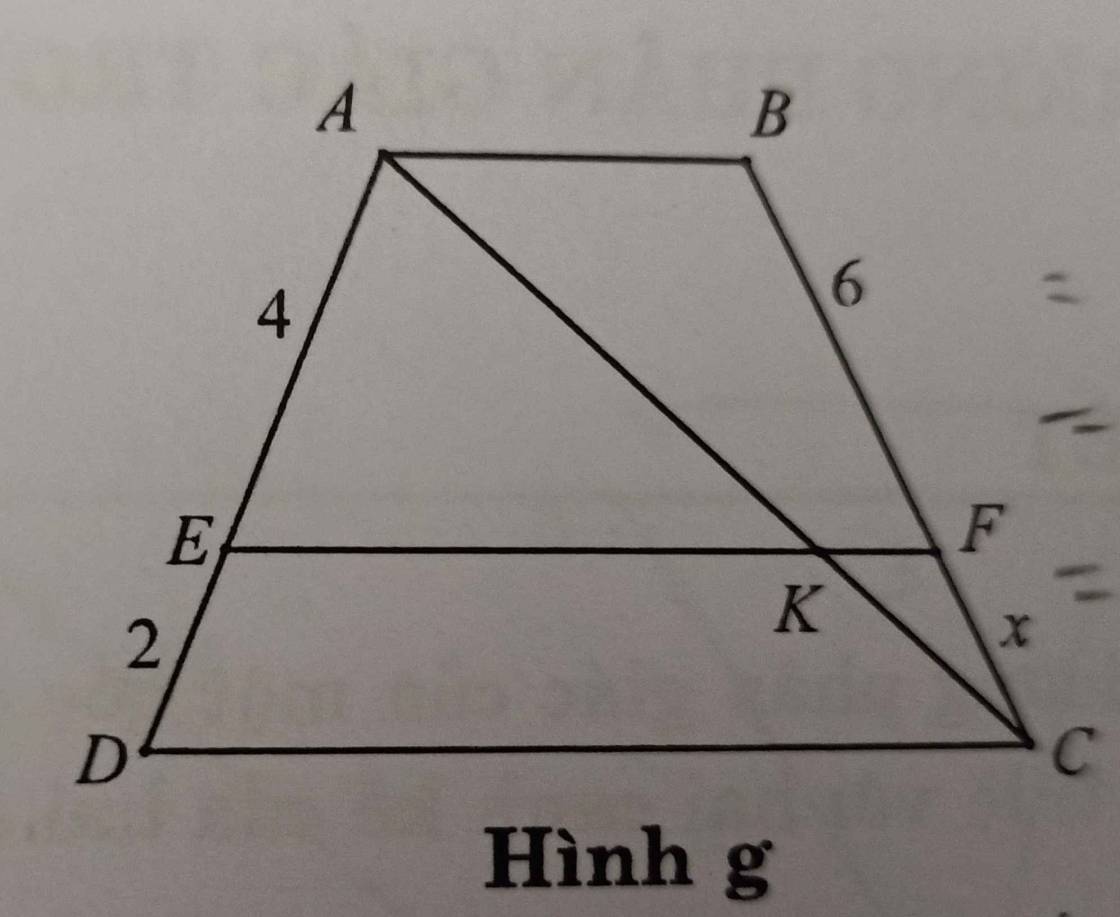



Hình f đề bài thiếu nên không tính được
Với hình g:
Áp dụng định lý Talet cho tam giác ADC:
\(\dfrac{AE}{ED}=\dfrac{AK}{KC}\Rightarrow\dfrac{AK}{KC}=\dfrac{4}{2}=2\)
\(\Rightarrow\dfrac{CK}{AK}=\dfrac{1}{2}\)
Áp dụng định lý Talet cho tam giác CAB:
\(\dfrac{CF}{BF}=\dfrac{CK}{AK}\Rightarrow\dfrac{x}{6}=\dfrac{1}{2}\Rightarrow x=3\)
Em cảm ơn nhìu ạ 😍❤️