Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(l=\dfrac{RS}{\rho}\Leftrightarrow R=\dfrac{l\rho}{S}\)
Cắt l thành n mảnh \(\Leftrightarrow l'=\dfrac{l}{4}\) \(\Leftrightarrow R'=\dfrac{\dfrac{l}{n}\rho}{S}=\dfrac{R}{n}=\dfrac{216}{n}\\ \Leftrightarrow R_{td}=\dfrac{R'.R'^n}{R'+R'^n}\Leftrightarrow6=\dfrac{\dfrac{216}{n}.\left(\dfrac{216}{n}\right)^n}{\dfrac{216}{n}+\left(\dfrac{216}{n}\right)^n}\Leftrightarrow n\approx0,27\)

Ta có: \(\dfrac{R}{R'}=\dfrac{\dfrac{p.l}{S}}{\dfrac{p.l'}{S}}=\dfrac{l}{l'}=\dfrac{l}{\dfrac{1}{2}l}=2\Rightarrow R'=\dfrac{R}{2}=\dfrac{8}{2}=4\left(\Omega\right)\)

\(MCD:R1ntR2\)
Điện trở tương đương của mạch:
\(R_{td}=R_1+R_2=20+30=50\Omega\)
Hiệu điện thế giữa hai đầu mỗi điện trở:
\(I=I_1=I_2=\dfrac{U}{R_{td}}=\dfrac{12}{50}=0,24A\Rightarrow\left\{{}\begin{matrix}U1=I1\cdot R1=0,24\cdot20=4,8V\\U2=I2\cdot R2=0,24\cdot30=7,2V\end{matrix}\right.\)
Nhiệt lượng toả ra của cả mạch trong 15 phút:
\(Q_{toa}=UIt=12\cdot0,24\cdot15\cdot60=2592\left(J\right)\)

a. \(R=R1+R2=3+6=9\Omega\)
\(I=I1=I2=U:R=18:9=2A\left(R1ntR2\right)\)
b. \(U_d=U_m=18V\Rightarrow\) mắc song song.
c. \(Q=A=UIt=Pt=9\cdot15\cdot60=8100\left(J\right)\)
\(I'=I+I_d=2+\left(\dfrac{9}{18}\right)=2,5A\)
\(\Rightarrow P=UI'=18.2,5=45\)W
a)Điện trở tương đương:
\(R_{tđ}=R_1+R_2=3+6=9\Omega\)
Do mắc nối tiếp nên \(I_1=I_2=I_m=\dfrac{18}{9}=2A\)
b)\(I_{Đđm}=\dfrac{P_Đ}{U_Đ}=\dfrac{9}{18}=0,5A\)
Để đèn sáng bình thường thì mắc đèn song song với hai điện trở.
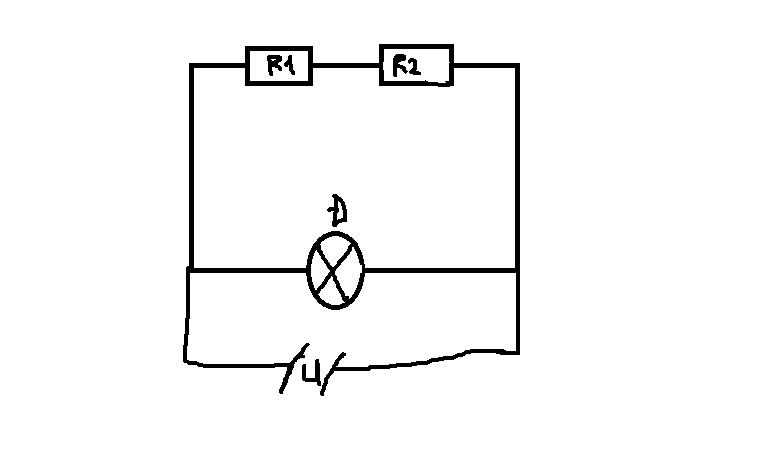
c)Nhiệt lượng tỏa ra trên đèn trong 10 phút:
\(Q=UIt=18\cdot0,5\cdot10\cdot60=5400J\)
Mắc bóng như câu b;
Điện trở đèn: \(R_Đ=\dfrac{18^2}{9}=36\Omega\)
\(I_Đ=\dfrac{U_m}{R_Đ}=\dfrac{18}{36}=0,5A\)
Công suất đèn lúc này: P=\(18\cdot0,5=9W\)

a. \(\left\{{}\begin{matrix}I=\dfrac{P}{U}=\dfrac{15}{12}=1,25A\\R=\dfrac{U}{I}=\dfrac{12}{1,25}=9,6\Omega\end{matrix}\right.\)
b. \(R_{td}=R+R_{bd}=10+9,6=19,6\Omega\)
c. \(R_{ss}=\dfrac{U}{I}=\dfrac{12}{5}=2,4\Omega\)
Ta có: \(\dfrac{1}{R_{ss}}=\dfrac{1}{R'}+\dfrac{1}{R''}=\dfrac{2}{R'}\Rightarrow R'=R''=2R_{ss}=2\cdot2,4=4,8\Omega\)