
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


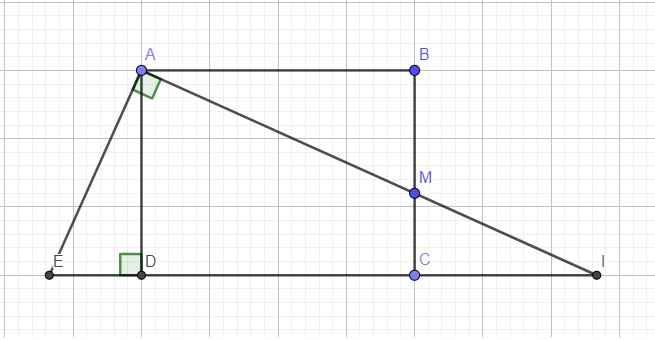
Qua A kẻ đường thẳng vuông góc AI cắt CD kéo dài tại E
Ta có \(\widehat{EAD}=\widehat{MAB}\) (cùng phụ \(\widehat{DAM}\))
\(\Rightarrow\Delta_vADE\sim\Delta_vABM\Rightarrow\dfrac{AE}{AM}=\dfrac{AD}{AB}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{AE}=\dfrac{4}{3AM}\)
Áp dụng hệ thức lượng trong tam giác vuông AEI:
\(\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AI^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{4}AB\right)^2}=\left(\dfrac{4}{3AM}\right)^2+\dfrac{1}{AI^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AM^2}+\dfrac{9}{16AI^2}\)

Bán kính đáy: 12:2=6(cm)
Thể tích nước dâng lên bằng thể tích tượng đá nên thể tích tượng đá là:
\(V=\pi.6^2.2,56\approx290\left(cm^3\right)=290\left(ml\right)\)

Đổi 1,672m= 167,2cm
167,2cm gấp 88cm số lần là:
167,2:88= 1,9(lần)
Bánh xe sau lăn được 50 vòng thì bánh xe trước lăn được:
50 x 1,9= 95(vòng)


3:
Tháng 4 phải trả:
\(50\cdot1678+50\cdot1734+100\cdot2014+100\cdot2536+1\cdot2834=628434\left(đồng\right)\)
Tháng 5 phải trả:
\(50\cdot1678+50\cdot1734+100\cdot2014+98\cdot2536=620528\left(đồng\right)\)
=>Giảm 1,3%

Bài 4:
a) Thay x=49 vào B ta có:
\(B=\dfrac{1-\sqrt{49}}{1+\sqrt{49}}=-\dfrac{3}{4}\)
b) \(A=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(A=\left[\dfrac{15-\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right]\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}-5}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}+1}\)
c) Ta có:
\(M=A-B=\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{1-1+\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}+1-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}=1-\dfrac{1}{\sqrt{x}+1}\)
Mà M nguyên khi:
\(1\) ⋮ \(\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;-1\right\}\)
Mà: \(\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}+1=1\)
\(\Rightarrow\sqrt{x}=0\)
\(\Rightarrow x=0\left(tm\right)\)
Vậy M nguyên khi x=0
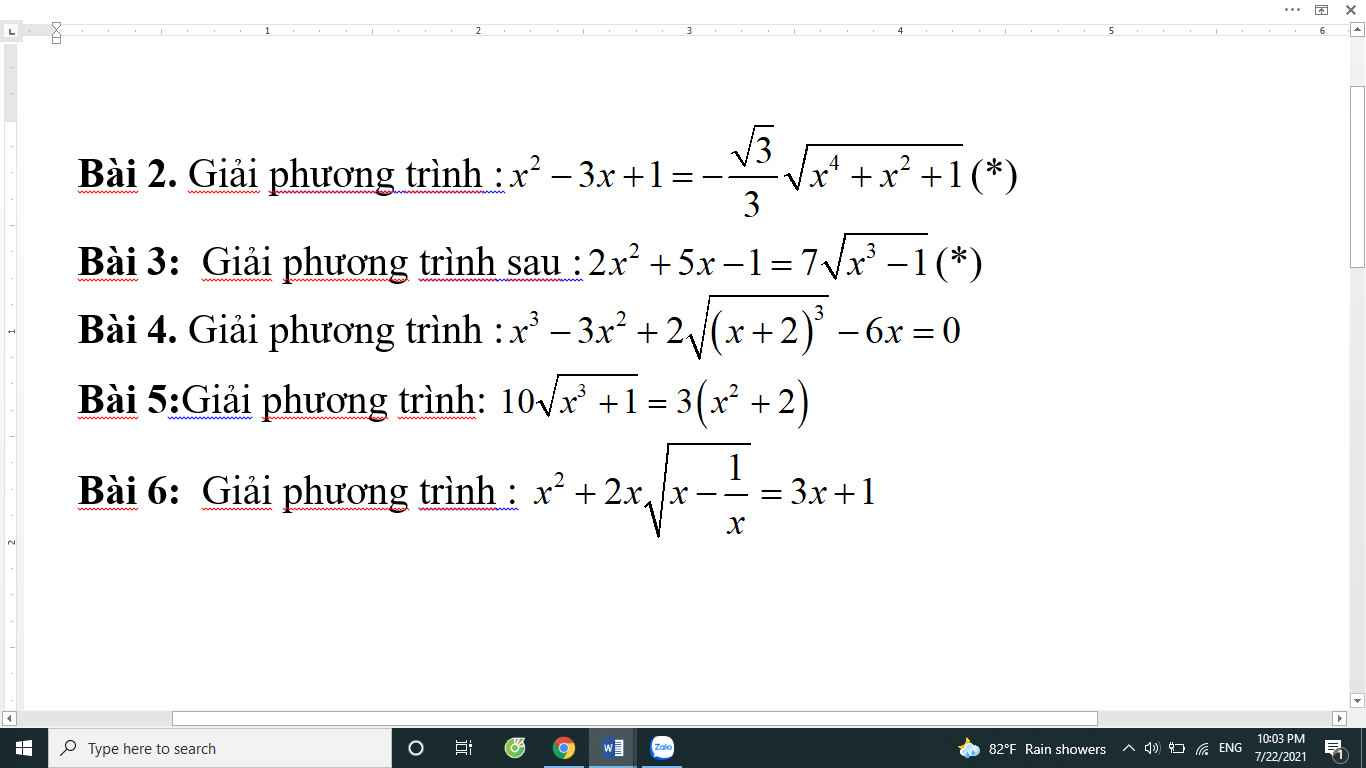




 làm giúp e câu 3, 4 với ạ
làm giúp e câu 3, 4 với ạ


 mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
Đặt \(\sqrt{x^2-x+1}=a>0;\sqrt{x^2+x+1}=b>0\).
\(PT\Leftrightarrow2a^2-b^2=-\dfrac{\sqrt{3}}{3}ab\)
\(\Leftrightarrow\left(a+\dfrac{\sqrt{3}}{2}b\right)\left(2a-\dfrac{2\sqrt{3}}{3}b\right)=0\)
\(\Leftrightarrow2a-\dfrac{2\sqrt{3}}{3}b=0\) (Do a, b > 0)
\(\Leftrightarrow2\sqrt{x^2-x+1}=\dfrac{2\sqrt{3}}{3}\sqrt{x^2+x+1}\)
\(\Leftrightarrow x^2-x+1=\dfrac{1}{3}\left(x^2+x+1\right)\Leftrightarrow2x^2-4x+2=0\Leftrightarrow x=1\).
Vậy x = 1