
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4\sin^22x-4\cos2x-1=0\)
\(\Leftrightarrow4\left(1-\cos^22x\right)-4\cos2x-1=0\)
\(\Leftrightarrow4-4\cos^22x-4\cos2x-1=0\)
\(\Leftrightarrow-4\cos^22x-4\cos2x+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\cos2x=\dfrac{-3}{2}\left(L\right)\end{matrix}\right.\Leftrightarrow\cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}-k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}-k\pi\end{matrix}\right.\left(k\in Z\right)\)
Chọn A

d.
\(y'=12x^2-1\)
e.
\(y'=\dfrac{\left(x-1\right)'\left(3x+1\right)-\left(3x+1\right)'\left(x-1\right)}{\left(3x+1\right)^2}=\dfrac{3x+1-3\left(x-1\right)}{\left(3x+1\right)^2}=\dfrac{4}{\left(3x+1\right)^2}\)
i.
\(y'=15x^2+\dfrac{1}{2\sqrt{x}}+\dfrac{12}{x^2}\)

\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+ax-2}-x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{ax-2}{\sqrt{x^2+ax-2}+x}=\lim\limits_{x\rightarrow+\infty}\dfrac{a-\dfrac{2}{x}}{\sqrt{1+\dfrac{a}{x}-\dfrac{2}{x^2}}+1}=\dfrac{a}{2}\)
\(\Rightarrow\dfrac{a}{2}=1\Rightarrow a=2\in\left(1;3\right)\)

\(y'=cos\sqrt{2+x^2}.\left(\sqrt{2+x^2}\right)'=cos\sqrt{2+x^2}.\dfrac{2x}{2\sqrt{2+x^2}}\)
\(=\dfrac{x}{\sqrt{2+x^2}}.cos\sqrt{2+x^2}\)
\(\Rightarrow m=1;n=0\)
\(\Rightarrow m+n=1\)

16.
\(\lim\dfrac{u_n}{v_n}=+\infty\)
17.
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB\Rightarrow\Delta SAB\) vuông tại A (B đúng)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (C đúng)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (D đúng)
18.
Tập hợp điểm cách đều 2 điểm AB cho trước là mặt phẳng trung trực của AB
19.
\(\lim\limits_{x\rightarrow1}\dfrac{x-1}{2x-2}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{2\left(x-1\right)}=\dfrac{1}{2}\)

21:
\(y'=\dfrac{\left(x^2-3x+5\right)'\left(x+2\right)-\left(x+2\right)'\left(x^2-3x+5\right)}{\left(x+2\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x+2\right)-\left(x^2-3x+5\right)}{\left(x+2\right)^2}\)
\(=\dfrac{2x^2+4x-3x-6-x^2+3x-5}{\left(x+2\right)^2}=\dfrac{x^2+4x-11}{\left(x+2\right)^2}\)
17:
Khi x<>0 thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\dfrac{1+4x-1}{\sqrt{1+4x}+1}\cdot\dfrac{1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{4}{\sqrt{1+4x}+1}=\dfrac{4}{1+1}=\dfrac{4}{2}=2\)
=>Chọn B






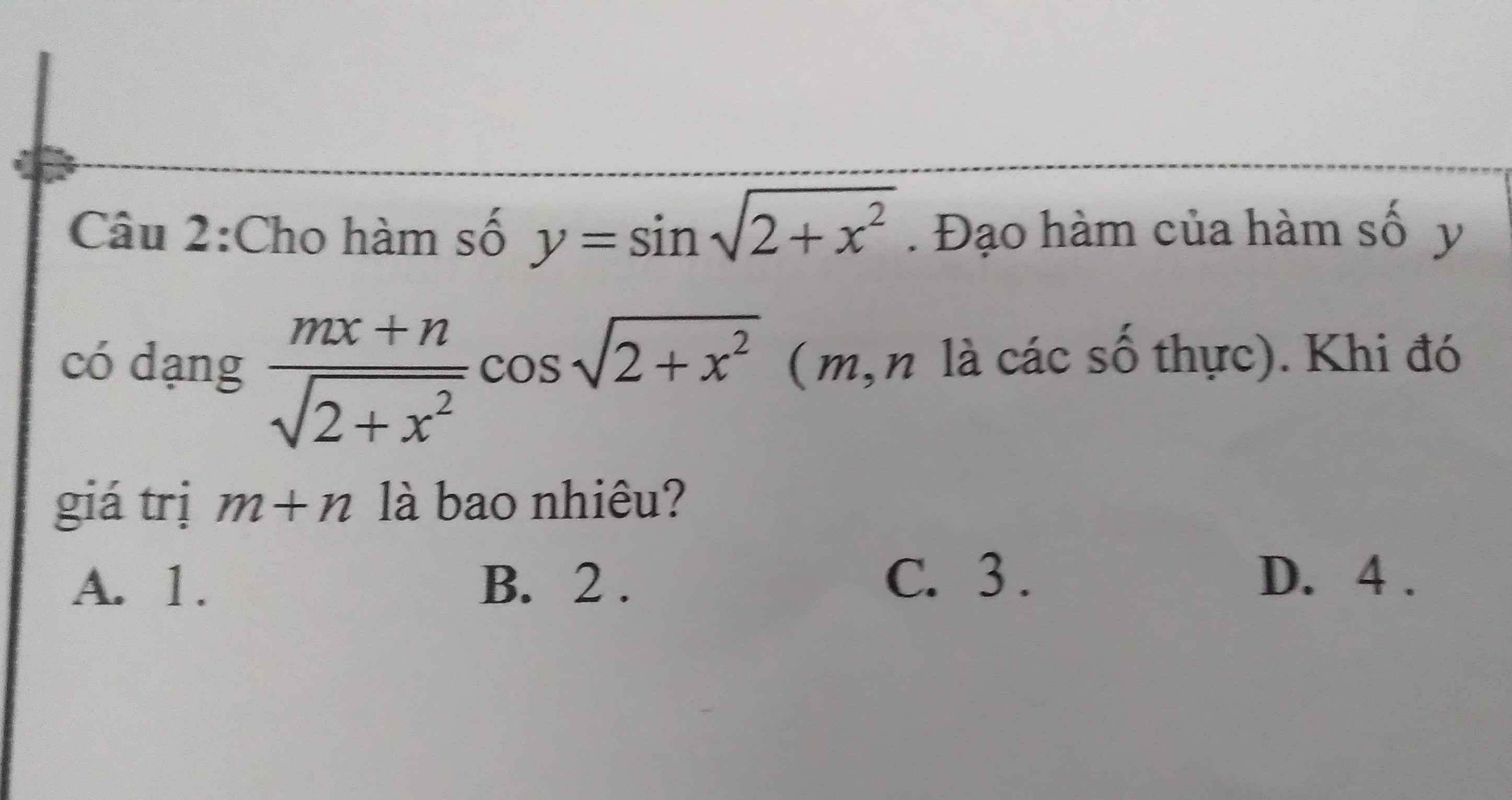





17.
Hàm có đúng 1 điểm gián đoạn khi và chỉ khi: \(x^2-2\left(m+3\right)x+9=0\) có đúng 1 nghiệm
\(\Rightarrow\Delta'=\left(m+3\right)^2-9=0\)
\(\Leftrightarrow m^2+6m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-6\end{matrix}\right.\)
\(\Rightarrow0+\left(-6\right)=-6\)