Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Không gian mẫu có dạng
Ω = {SSS, SSN, SNS, NSS, SNN, NSN, NNS, NNN}
b)
A = {SSS, SNS, SSN, SNN};
B = {SSS, NNN};
C = {SSN, SNS, NSS};
D = {NN N } = Ω \ {NNN}.
Không gian (KG) mẫu: gồm 8 phần tử
Ω = {SSS, SSN, SNS, SNN, NSS, NSN, NNS, NNN}.
Trong đó SSS là kết quả "ba lần gieo đồng tiền xuất hiện mặt sấp"; NSS là kết quả "lần đầu đồng tiền xuất hiện mặt ngửa, lần thứ 2, lần thứ 3 xuất hiện mặt sấp"
b) A = {SSS, SSN, SNS, SNN},
B = {SNN, NSN, NNS},
C = {SSN, SNS, SNN, NSS, NSN, NNS, NNN} = Ω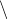 
{SSS}.
a. Không gian mẫu của phép thử gồm 5 phần tử được mô tả sau:
Ω = {S, NS, NNS, NNNS, NNNN}
b. Xác định các biến cố:
+ A: "Số lần gieo không vượt quá 3"
A = {S, NS, NNS}
+ B: "Số lần gieo là 4"
B = {NNNS, NNNN}.
b. Biến cố C: “ Có ít nhất hai đồng tiền xuất hiện mặt ngửa” tức là có thể có hai hoặc ba đồng tiền xuất hiện mặt ngửa. Vì vậy chọn phương án B
Kết quả của 5 lần gieo mà mặt N xuất hiện đúng một lần: 
Kết quả của 5 lần gieo mà mặt N xuất hiện đúng hai lần: 
Số kết quả của 5 lần gieo mà số lần mặt S xuất hiện nhiều hơn số lần mặt N là: 
Chọn C
a) Ω = {S1, S2, S3, S4, S5, N1, N2, N3, N4, N5}
b)
A = {S2, S4, S6};
B = {N1, N3, N5}.
Kết quả 5 lần gieo mà không có lần nào xuất hiện mặt sấp là 1
Vậy n(B) = 32 - 1 = 31.
Chọn A.
Biến cố A: "Cả 3 lần xuất hiện mặt sấp"
=>\(A=\left\{A_1;A_2;A_3\right\}\)
Biến cố B: "Cả 3 lần xuất hiện mặt ngửa"
=>\(B=\left\{\overline{A_1};\overline{A_2};\overline{A_3}\right\}\)
a. Kí hiệu : S là đồng tiền ra mặt sấp và N là đồng tiền ra mặt ngửa
Không gian mẫu gồm 8 phần tử:
Ω = {SSS, SSN, NSS, SNS, NNS, NSN, SNN, NNN}
b.Xác định các biến cố:
A:"Lần đầu xuất hiện mặt sấp"
A ={SSS, SSN, SNS, SNN}
B: "Mặt sấp xảy ra đúng một lần"
B = {SNN, NSN, NNS}
C: "Mặt ngửa xảy ra ít nhất một lần".
C = {SSN, NSS, SNS, NNS, NSN, SNN, NNN}