Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Do hai nguồn u A và u B vuông pha với nhau nên sóng truyền từ A đến trung điểm của AB vuông pha với sóng truyền từ B đến trung điểm của AB → quy về bài toán tổng hợp hai dao động vuông pha → phần tử vật chất tại trung điểm AB dao động với biên độ 3 a 2 + 4 a 2 = 5 a .

Đáp án B
Do hai nguồn uA và uB vuông pha với nhau nên sóng truyền từ A đến trung điểm của AB vuông pha với sóng truyền từ B đến trung điểm của AB → quy về bài toán tổng hợp hai dao động vuông pha → phần tử vật chất tại trung điểm AB dao động với biên độ ( 3 a ) 2 + ( 4 a ) 2 = 5 a .

Chọn A
Phần tử vật chất tại trung điểm AB sẽ có 2 sóng thành phần lệch pha giống như độ lệch pha của 2 nguồn ,tại đây 2 sóng thành phần ngược pha nhau

Chọn A

trên đoạn AB có 5 “bó sóng” vớ O là bụng của bó trung tâm. Các bó đối xứng nhau qua một bụng thì cùng pha nên có hai điểm khác cùng pha với O

\(u_1=a.\cos\left(wt\right)\)
\(u_2=a.cos\left(wt+\pi\right)\)
Nhận thấy A và B là nguồn ngược pha.
Gọi M là trung điểm của A và B => \(d_1=AM\Rightarrow d_2=BM\)
Biên độ giao động tại M :
\(A_M=\left|2a\cos\left(\frac{\varphi_1-\varphi_2}{2}+\frac{\pi\left(d_2-d_1\right)}{\lambda}\right)\right|\)
\(\Rightarrow A_M=\left|2a\sin\frac{\pi\left(d_1-d_2\right)}{\lambda}\right|\)
Mà d1 = d2
=> AM =0

Đáp án: A
HD Giải: λ = 80 2 π 100 π = 1,6cm
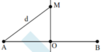
M cùng pha với nguồn A nên MA = d = (được rút ra từ phương trình sóng tại M với d1 = d2 = d)
Ta có điều kiện MA > AO = AB/2 nên
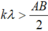
<=> 1,6k > 6
<=> k > 3,75
MA nhỏ nhất nên chọn k = 4
MA = 4.1,6 = 6,4 cm
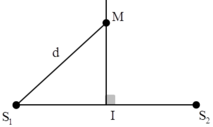

Hai nguồn ngược pha → Trung điểm của đường thẳng nối hai nguồn dao động với biên độ cực tiểu a = 0.
Đáp án B